4 Funciones de Activación (Activation Functions)

“Si sabes exactamente lo que estás haciendo, no es investigación.” - Albert Einstein

En la historia del aprendizaje profundo, las funciones de activación y las técnicas de optimización han logrado un desarrollo muy importante. Cuando el modelo de neurona artificial de McCulloch-Pitts apareció por primera vez en 1943, solo se utilizaba una función umbral simple (función escalón). Esto imitaba la forma en que los neuronas biológicos se activan solo cuando las entradas superan un cierto umbral. Sin embargo, este tipo de funciones de activación simples limitaban la capacidad de las redes neuronales para representar funciones complejas.

Hasta la década de 1980, el aprendizaje automático se centraba en el diseño de ingeniería de características y algoritmos sofisticados. Las redes neuronales eran solo una de varias técnicas de aprendizaje automático, y los algoritmos tradicionales como las Máquinas de Vector Soporte (SVM) o los Bosques Aleatorios a menudo mostraban un rendimiento superior. Por ejemplo, en el problema de reconocimiento de escritura manual MNIST, las SVM mantuvieron la mejor precisión hasta 2012.

En 2012, AlexNet logró un rendimiento sobresaliente en el desafío ImageNet gracias a su aprendizaje eficiente utilizando GPU, lo que marcó el comienzo oficial de la era del aprendizaje profundo. En 2017, la arquitectura Transformer de Google avanzó aún más esta innovación y se convirtió en la base de los modelos de lenguaje a gran escala (LLM) actuales como GPT-4 y Gemini.

En el centro de estos avances estuvieron la evolución de las funciones de activación y el desarrollo de técnicas de optimización. En este capítulo, examinaremos en detalle las funciones de activación con el objetivo de proporcionar una base teórica sólida para que puedas desarrollar nuevos modelos y resolver problemas complejos.

4.1 Funciones de Activación: Introduciendo No Linealidad a las Redes Neuronales

Dilema del Investigador: Los investigadores de redes neuronales iniciales se dieron cuenta de que solo con transformaciones lineales no podían resolver problemas complejos. Sin embargo, no estaba claro qué función no lineal debería usarse para que las redes neuronales aprendan eficazmente y resuelvan una variedad de problemas. ¿Imitar el funcionamiento de los neuronas biológicos es la mejor opción? ¿O hay otras funciones con características matemáticas y computacionales más adecuadas?

4.1.1 Por qué se Necesitan Funciones de Activación: Superando las Limitaciones de Linealidad

Sin funciones de activación, no importa cuántas capas agregues, la red neuronal seguirá siendo simplemente una transformación lineal. Esto puede demostrarse fácilmente.

Consideremos el caso de aplicar dos transformaciones lineales consecutivamente:

Primera capa: \(y_1 = W_1x + b_1\)
Segunda capa: \(y_2 = W_2y_1 + b_2\)

Aquí, \(x\) es la entrada, \(W_1\), \(W_2\) son matrices de pesos, y \(b_1\), \(b_2\) son vectores de sesgo. Sustituyendo la ecuación de la primera capa en la segunda:

\(y_2 = W_2(W_1x + b_1) + b_2 = (W_2W_1)x + (W_2b_1 + b_2)\)

Definamos una nueva matriz de pesos \(W' = W_2W_1\) y un nuevo vector de sesgo \(b' = W_2b_1 + b_2\), entonces:

\(y_2 = W'x + b'\)

Esto es, al final, equivalente a una sola transformación lineal. Lo mismo ocurre independientemente del número de capas. Por lo tanto, solo con transformaciones lineales no se puede representar relaciones no lineales complejas. ### 4.1.2 Evolución de las funciones de activación: desde la imitación biológica hasta el cálculo eficiente

1943, Neurona McCulloch-Pitts: En el primer modelo de neurona artificial se utilizó una función umbral (threshold function) simple, es decir, una función escalón (step function). Esta fue una imitación del modo en que las neuronas biológicas se activan solo cuando la entrada supera un umbral específico.

\[ f(x) = \begin{cases} 1, & \text{si } x \ge \theta \\ 0, & \text{si } x < \theta \end{cases} \]

Aquí, \(\theta\) es el umbral.
Década de 1960, Función Sigmoide (Sigmoid): Para modelar de manera más suave la tasa de disparo (firing rate) de las neuronas biológicas, se introdujo la función sigmoide. La función sigmoide tiene una curva en forma de S y comprime los valores de entrada entre 0 y 1.

\[ \sigma(x) = \frac{1}{1 + e^{-x}} \]

La ventaja de la función sigmoide es que es diferenciable, lo que permitió aplicar algoritmos de aprendizaje basados en el descenso del gradiente (gradient descent). Sin embargo, se ha identificado a la función sigmoide como una de las causas del problema del desvanecimiento del gradiente (vanishing gradient problem) en redes neuronales profundas. Cuando los valores de entrada son muy grandes o muy pequeños, la pendiente (valor de la derivada) de la función sigmoide se aproxima a 0, lo que puede ralentizar o detener el aprendizaje.
2010, ReLU (Rectified Linear Unit): Nair y Hinton propusieron la función ReLU, abriendo una nueva era en el aprendizaje de redes neuronales profundas. La forma de ReLU es muy simple.

\[ ReLU(x) = \max(0, x) \]

ReLU devuelve el valor de entrada si es mayor que 0, y 0 si es menor que 0. A diferencia de la función sigmoide, ReLU tiene menos probabilidades de causar el problema del desvanecimiento del gradiente y es más eficiente en términos de cálculo. Estas ventajas han contribuido significativamente al éxito de las redes neuronales profundas, y ReLU es una de las funciones de activación más utilizadas actualmente.

4.1.3 Selección de las funciones de activación: tamaño del modelo, tarea y eficiencia

La elección de la función de activación tiene un gran impacto en el rendimiento y la eficiencia del modelo.

Modelos de lenguaje a gran escala (LLM): Debido a la importancia de la eficiencia computacional, tienden a preferir funciones de activación simples. Modelos recientes como Llama 3, GPT-4 y Gemini han adoptado funciones de activación simples y eficientes, como GELU (Gaussian Error Linear Unit) o ReLU. En particular, Gemini 1.5 ha introducido la arquitectura MoE (Mixture of Experts), que utiliza funciones de activación optimizadas para cada red experta.
Modelos de propósito específico: Al desarrollar modelos optimizados para tareas específicas, a veces se intentan enfoques más sofisticados. Por ejemplo, investigaciones recientes como TEAL han propuesto métodos para mejorar la velocidad de inferencia hasta 1.8 veces mediante la activación de la esparsidad (activation sparsity). También hay estudios que utilizan funciones de activación adaptativas (adaptive activation functions) que ajustan su comportamiento dinámicamente según los datos de entrada.

La elección de la función de activación debe considerar de manera integral el tamaño del modelo, las características de la tarea, los recursos computacionales disponibles y las características de rendimiento requeridas (precisión, velocidad, uso de memoria, etc.).

4.2 Comparación de funciones de activación

Desafío: ¿Cuál de las numerosas funciones de activación es la más adecuada para un problema y arquitectura específicos?

Angustia del investigador: En 2025, se han propuesto más de 500 funciones de activación, pero no existe una función perfecta para todas las situaciones. Los investigadores deben comprender las características de cada función, y considerar las características del problema, la arquitectura del modelo, los recursos computacionales, etc., para seleccionar la función de activación óptima o incluso desarrollar nuevas funciones.

Las propiedades generalmente requeridas en una función de activación son las siguientes: 1. Debe agregar curvatura no lineal a la red neuronal. 2. No debe aumentar la complejidad computacional hasta el punto de dificultar el entrenamiento. 3. Debe ser diferenciable para no obstaculizar el flujo del gradiente. 4. Los datos en cada capa de la red neuronal deben tener una distribución adecuada durante el entrenamiento.

Se han propuesto muchas funciones de activación eficientes que cumplen con estos requisitos. No es fácil decir cuál es la mejor función de activación, ya que depende del modelo y los datos a entrenar. El método para encontrar la función de activación óptima es realizar pruebas prácticas.

En 2025, las funciones de activación se clasifican en tres categorías principales: 1. Funciones de activación clásicas: Sigmoid, Tanh, ReLU, entre otras, que tienen una forma fija. 2. Funciones de activación adaptativas: PReLU, TeLU, STAF, que incluyen parámetros ajustables durante el proceso de aprendizaje. 3. Funciones de activación especializadas: ENN (Expressive Neural Network), funciones de activación informadas por la física, optimizadas para dominios específicos.

En este capítulo, comparamos varias funciones de activación. Nos centraremos principalmente en las implementaciones disponibles en PyTorch, pero crearemos nuevas clases heredando de nn.Module para funciones como Swish y STAF que no están implementadas. El código completo se encuentra en chapter_04/models/activations.py.

4.2.1 Creación de funciones de activación

Code

!pip install dldna[colab] # in Colab
# !pip install dldna[all] # in your local

%load_ext autoreload
%autoreload 2

Code

import torch
import torch.nn as nn
import numpy as np

# Set seed
np.random.seed(7)
torch.manual_seed(7)

# STAF (Sinusoidal Trainable Activation Function)
class STAF(nn.Module):
    def __init__(self, tau=25):
        super().__init__()
        self.tau = tau
        self.C = nn.Parameter(torch.randn(tau))
        self.Omega = nn.Parameter(torch.randn(tau))
        self.Phi = nn.Parameter(torch.randn(tau))

    def forward(self, x):
        result = torch.zeros_like(x)
        for i in range(self.tau):
            result += self.C[i] * torch.sin(self.Omega[i] * x + self.Phi[i])
        return result

# TeLU (Trainable exponential Linear Unit)
class TeLU(nn.Module):
    def __init__(self, alpha=1.0):
        super().__init__()
        self.alpha = nn.Parameter(torch.tensor(alpha))

    def forward(self, x):
        return torch.where(x > 0, x, self.alpha * (torch.exp(x) - 1))

# Swish (Custom Implementation)
class Swish(nn.Module):
    def forward(self, x):
        return x * torch.sigmoid(x)

# Activation function dictionary
act_functions = {
    # Classic activation functions
    "Sigmoid": nn.Sigmoid,     # Binary classification output layer
    "Tanh": nn.Tanh,          # RNN/LSTM

    # Modern basic activation functions
    "ReLU": nn.ReLU,          # CNN default
    "GELU": nn.GELU,          # Transformer standard
    "Mish": nn.Mish,          # Performance/stability balance

    # ReLU variants
    "LeakyReLU": nn.LeakyReLU,# Handles negative inputs
    "SiLU": nn.SiLU,          # Efficient sigmoid
    "Hardswish": nn.Hardswish,# Mobile optimized
    "Swish": Swish,           # Custom implementation

    # Adaptive/trainable activation functions
    "PReLU": nn.PReLU,        # Trainable slope
    "RReLU": nn.RReLU,        # Randomized slope
    "TeLU": TeLU,             # Trainable exponential
    "STAF": STAF             # Fourier-based
}

STAF es la función de activación más reciente introducida en ICLR 2025, que utiliza parámetros aprendibles basados en series de Fourier. ENN adopta un método que aprovecha la DCT para mejorar la expresividad de la red. TeLU es una versión extendida de ELU que hace el parámetro alpha aprendible.

4.2.2 Perspectiva visual de las funciones de activación

Se comparan características al visualizar las funciones de activación y sus gradientes. Utilizando la función de diferenciación automática de PyTorch, se pueden calcular fácilmente los gradientes con una llamada a backward(). A continuación se presenta un ejemplo de análisis visual de las características de las funciones de activación. El cálculo del flujo de gradiente se realiza mediante la entrada de valores en un rango constante para la función de activación dada. El método que realiza esta tarea es compute_gradient_flow.

Code

def compute_gradient_flow(activation, x_range=(-5, 5), y_range=(-5, 5), points=100):
    """
    Computes the 3D gradient flow.

    Calculates the output surface of the activation function for two-dimensional
    inputs and the magnitude of the gradient with respect to those inputs.

    Args:
        activation: Activation function (nn.Module or function).
        x_range (tuple): Range for the x-axis (default: (-5, 5)).
        y_range (tuple): Range for the y-axis (default: (-5, 5)).
        points (int): Number of points to use for each axis (default: 100).

    Returns:
        X, Y (ndarray): Meshgrid coordinates.
        Z (ndarray): Activation function output values.
        grad_magnitude (ndarray): Gradient magnitude at each point.
    """
    x = np.linspace(x_range[0], x_range[1], points)
    y = np.linspace(y_range[0], y_range[1], points)
    X, Y = np.meshgrid(x, y)

    # Stack the two dimensions to create a 2D input tensor (first row: X, second row: Y)
    input_tensor = torch.tensor(np.stack([X, Y], axis=0), dtype=torch.float32, requires_grad=True)

    # Construct the surface as the sum of the activation function outputs for the two inputs
    Z = activation(input_tensor[0]) + activation(input_tensor[1])
    Z.sum().backward()

    grad_x = input_tensor.grad[0].numpy()
    grad_y = input_tensor.grad[1].numpy()
    grad_magnitude = np.sqrt(grad_x**2 + grad_y**2)

Realiza una visualización 3D para todas las funciones de activación definidas.

Code

from dldna.chapter_04.visualization.activations import visualize_all_activations

visualize_all_activations()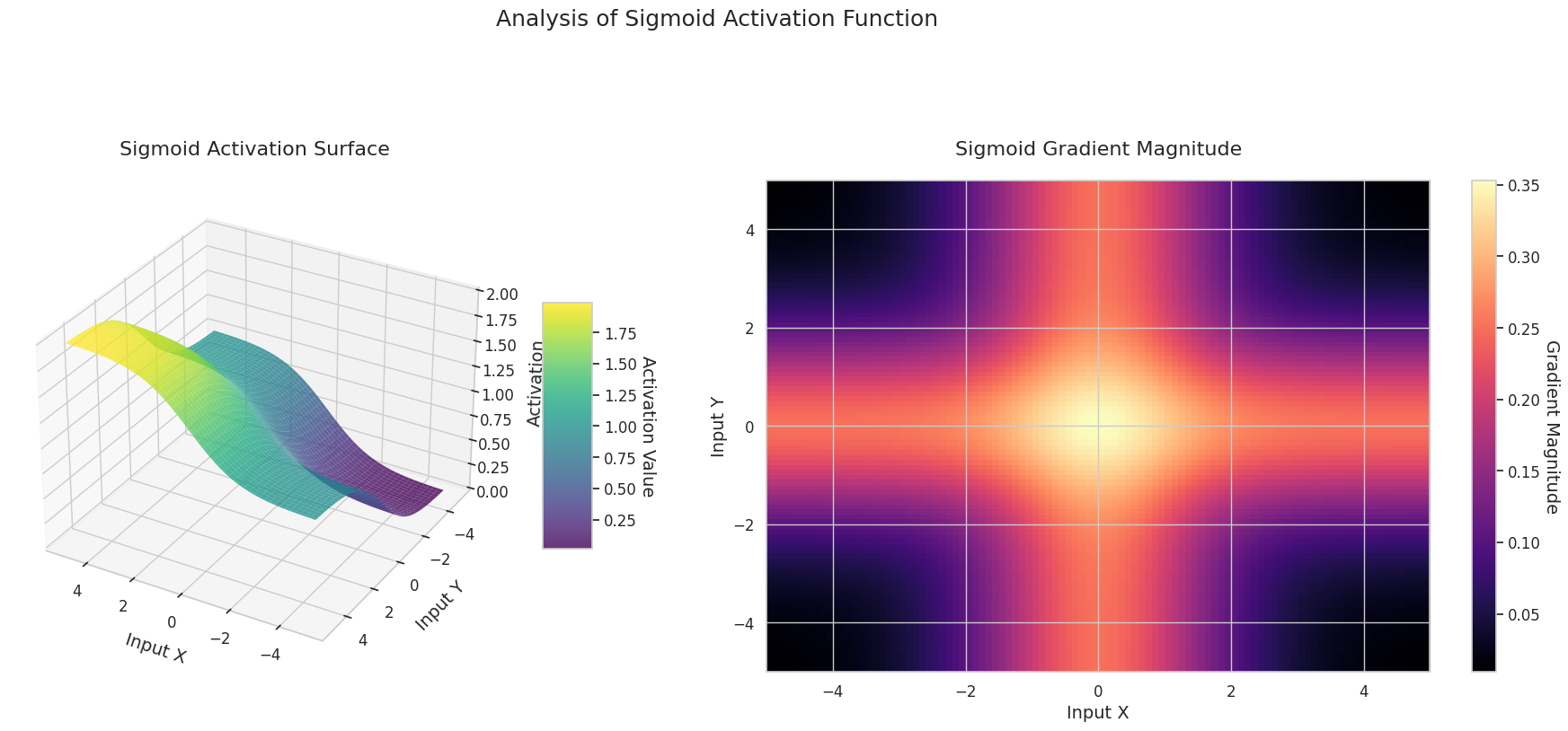

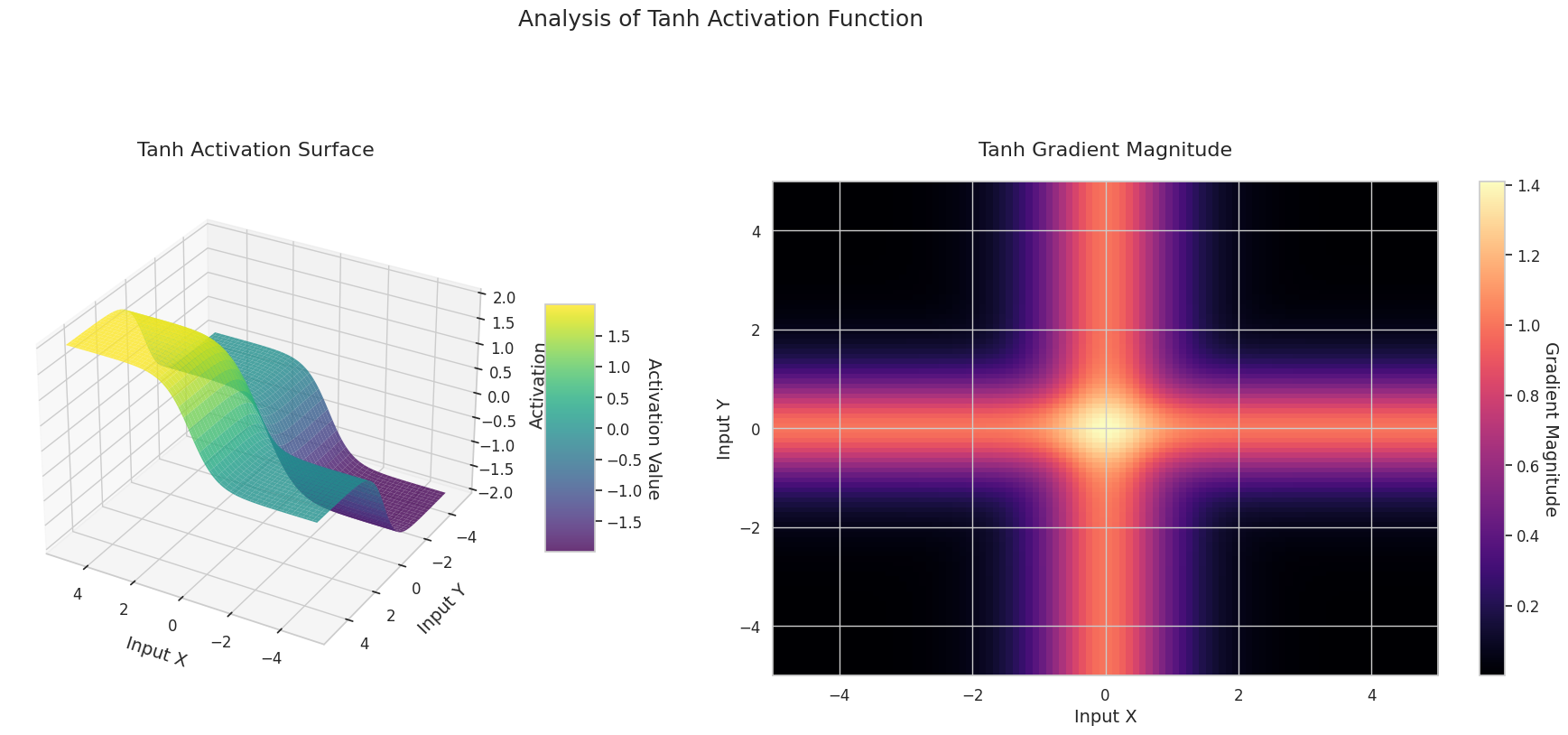
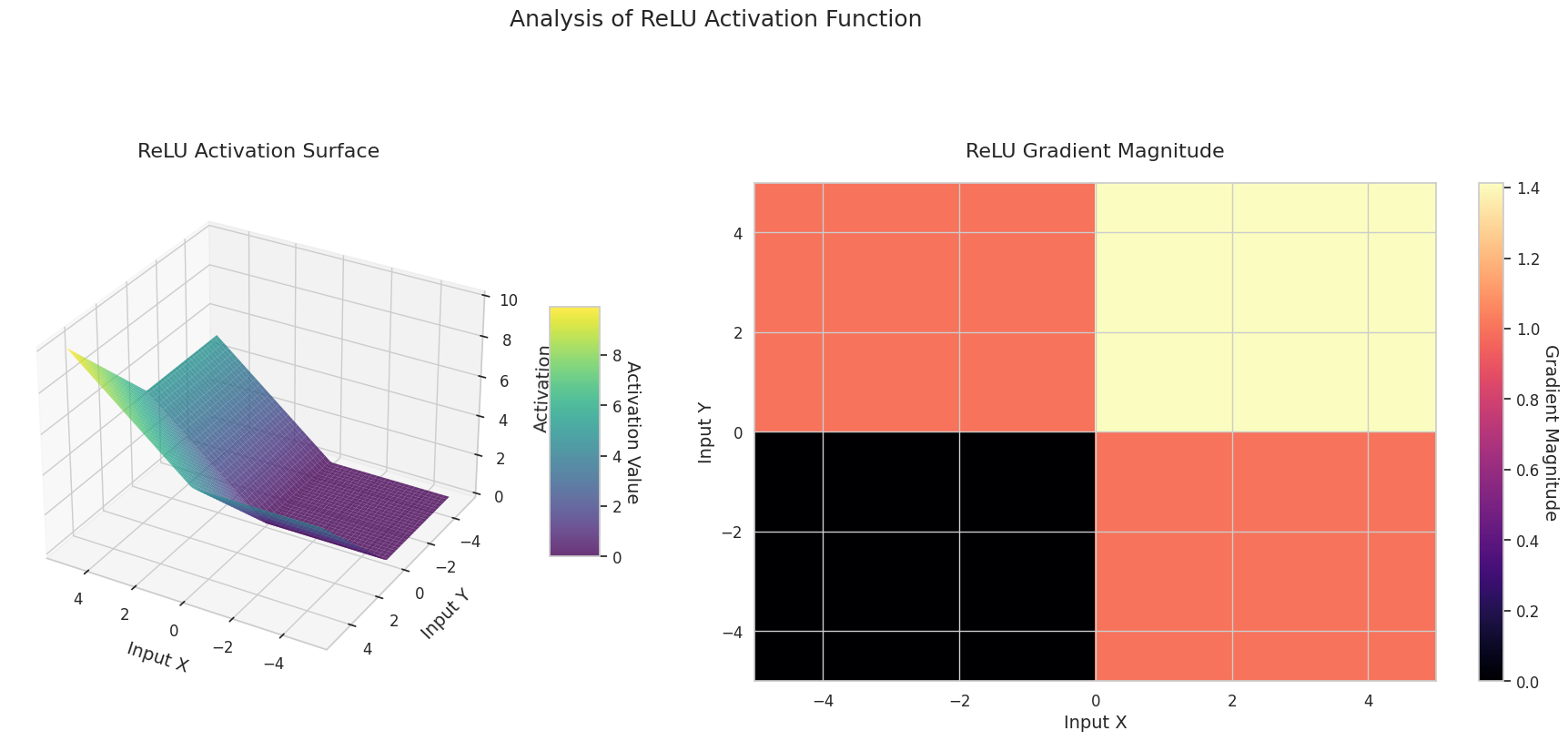
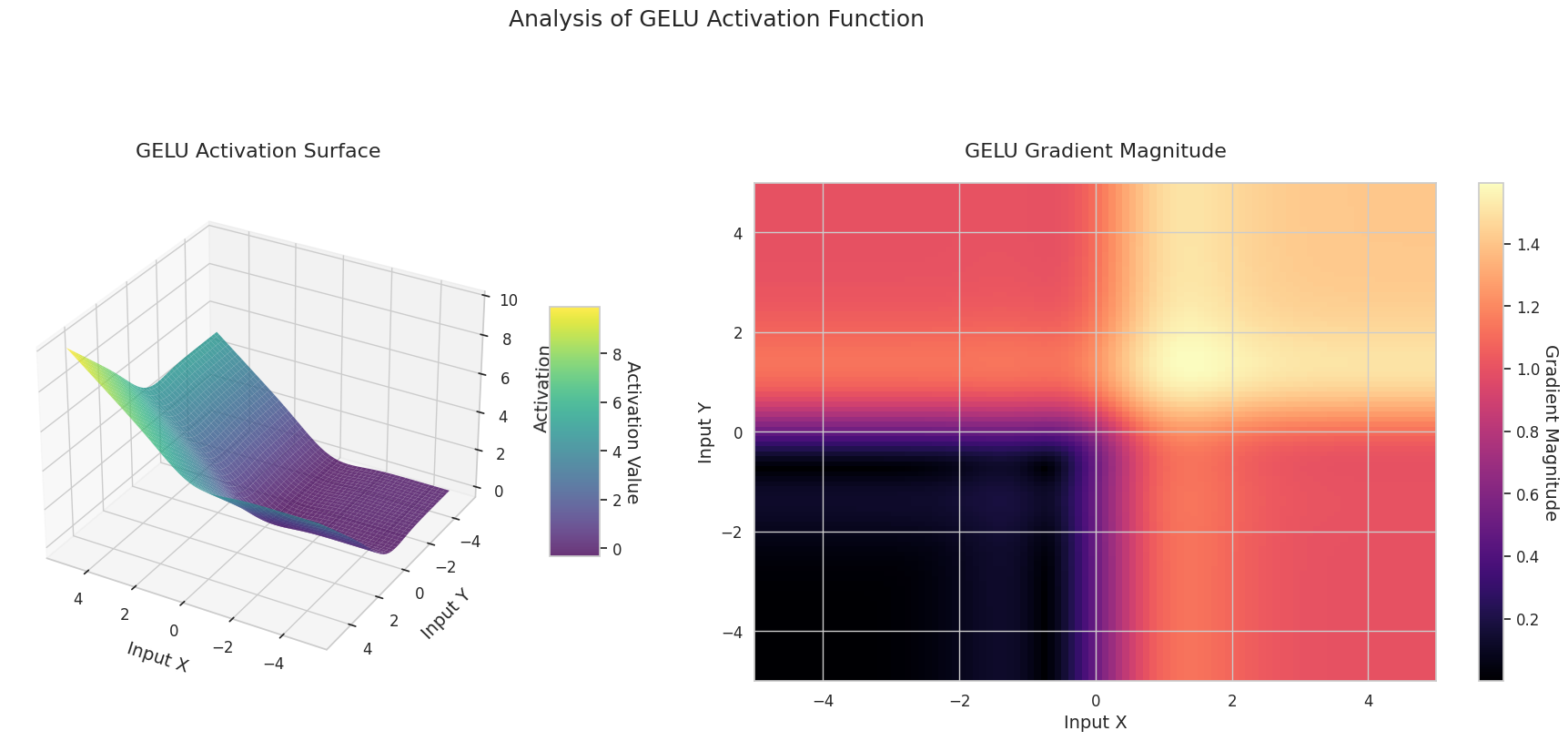
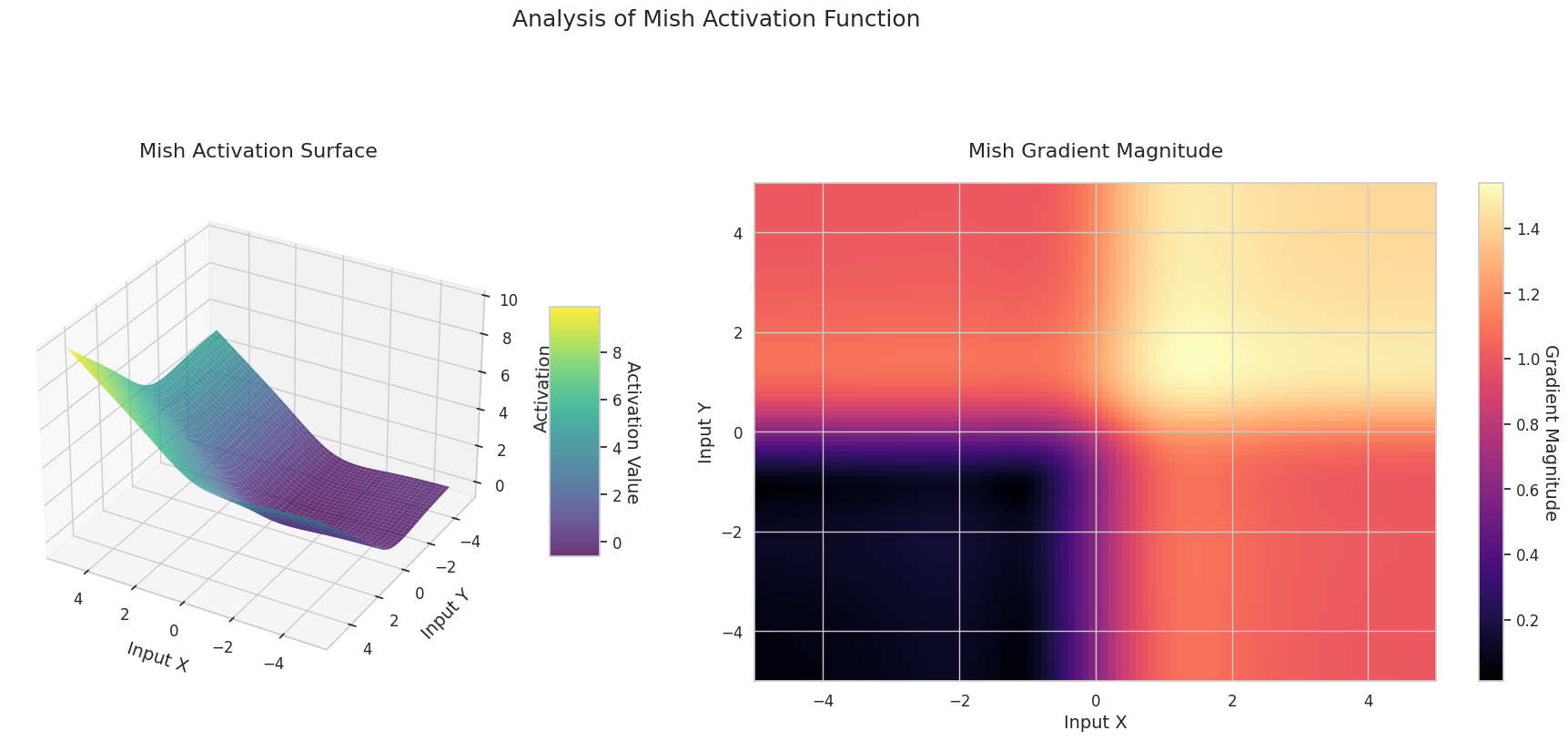
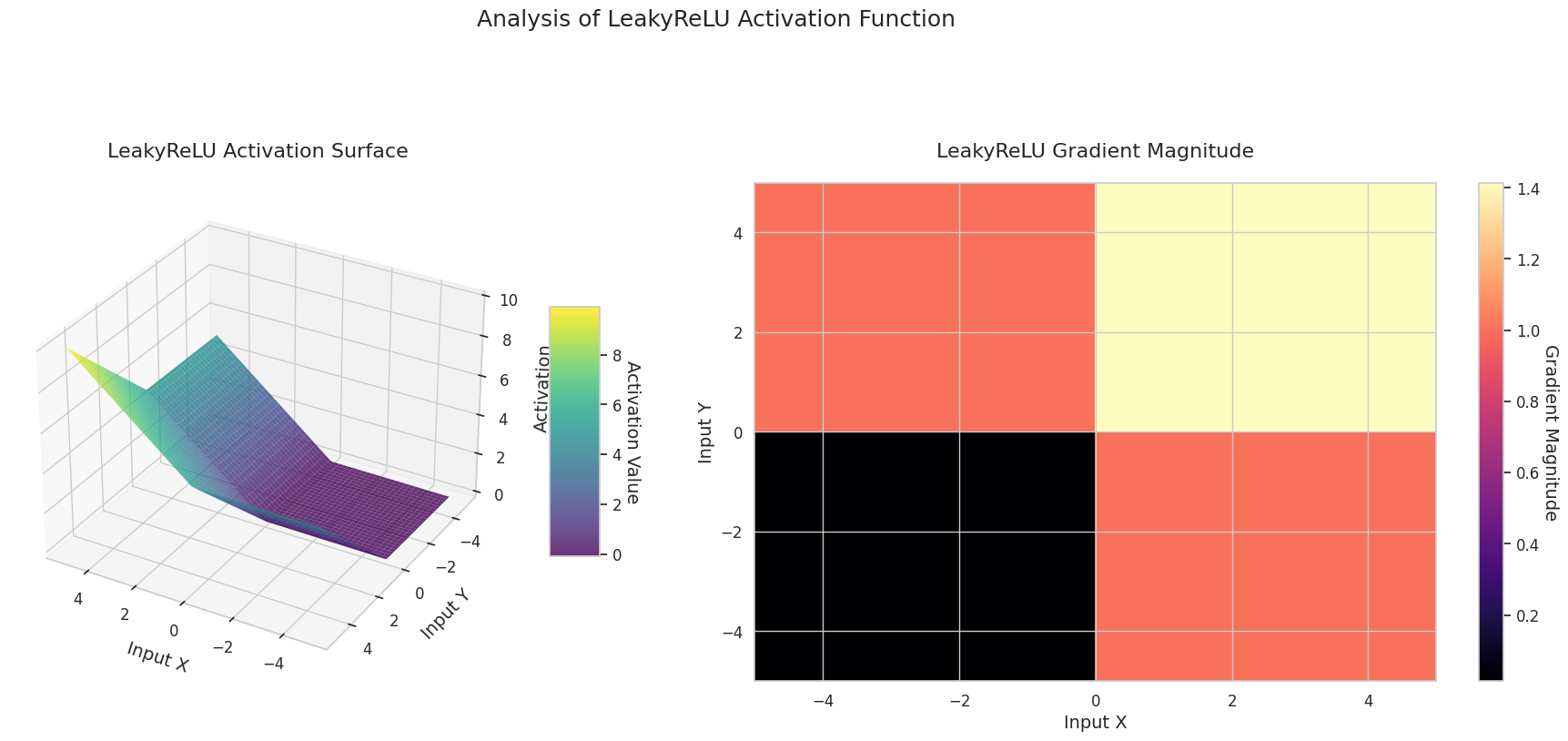
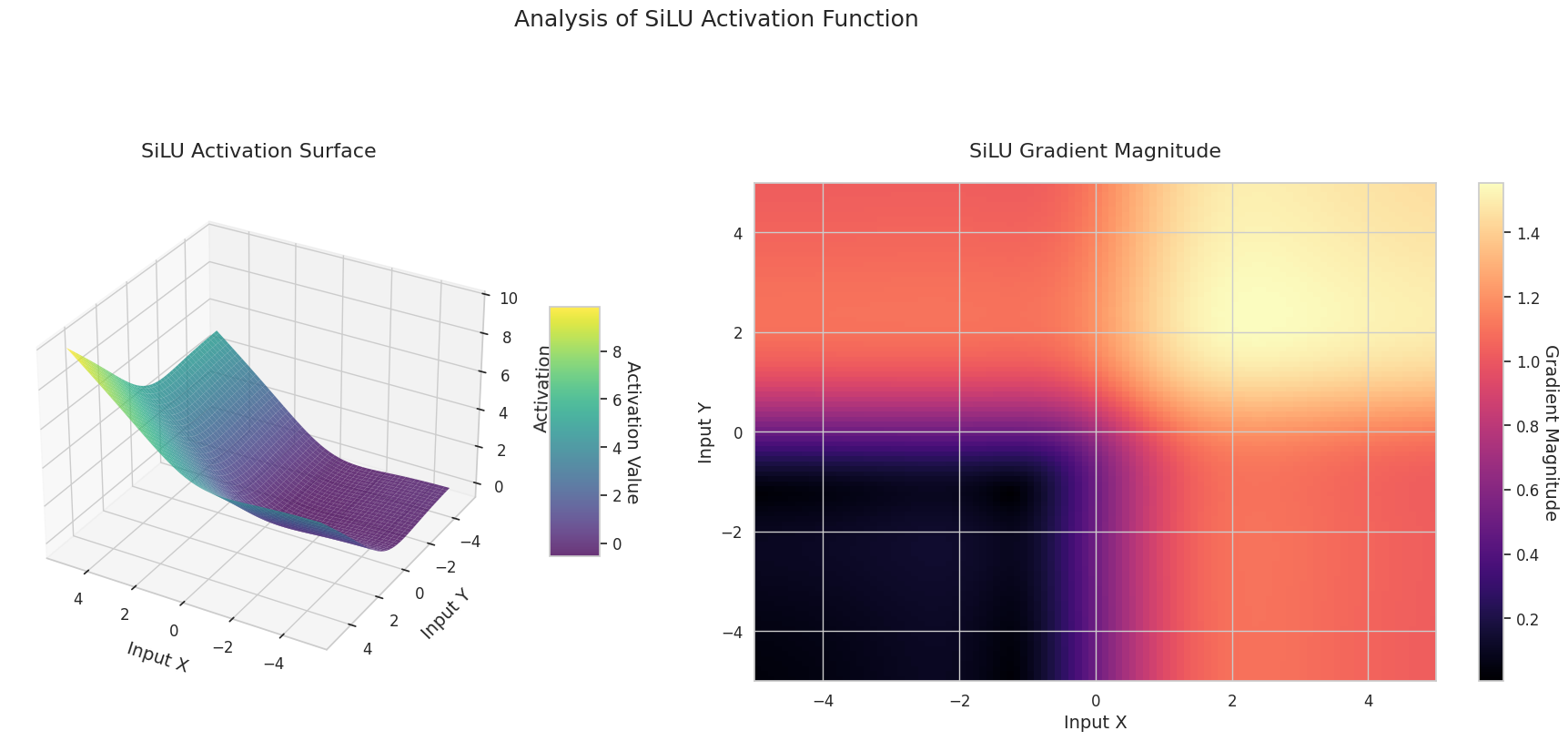
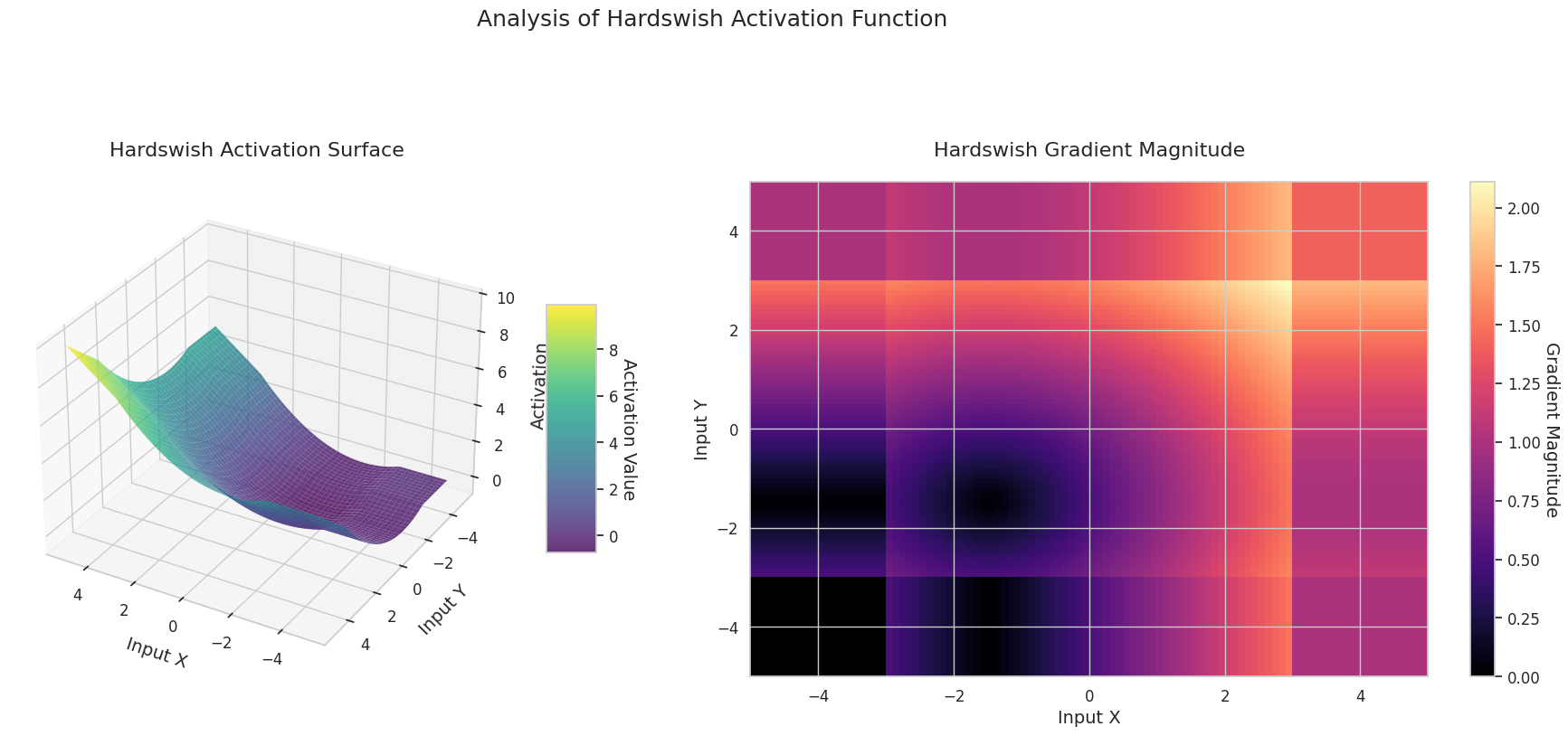
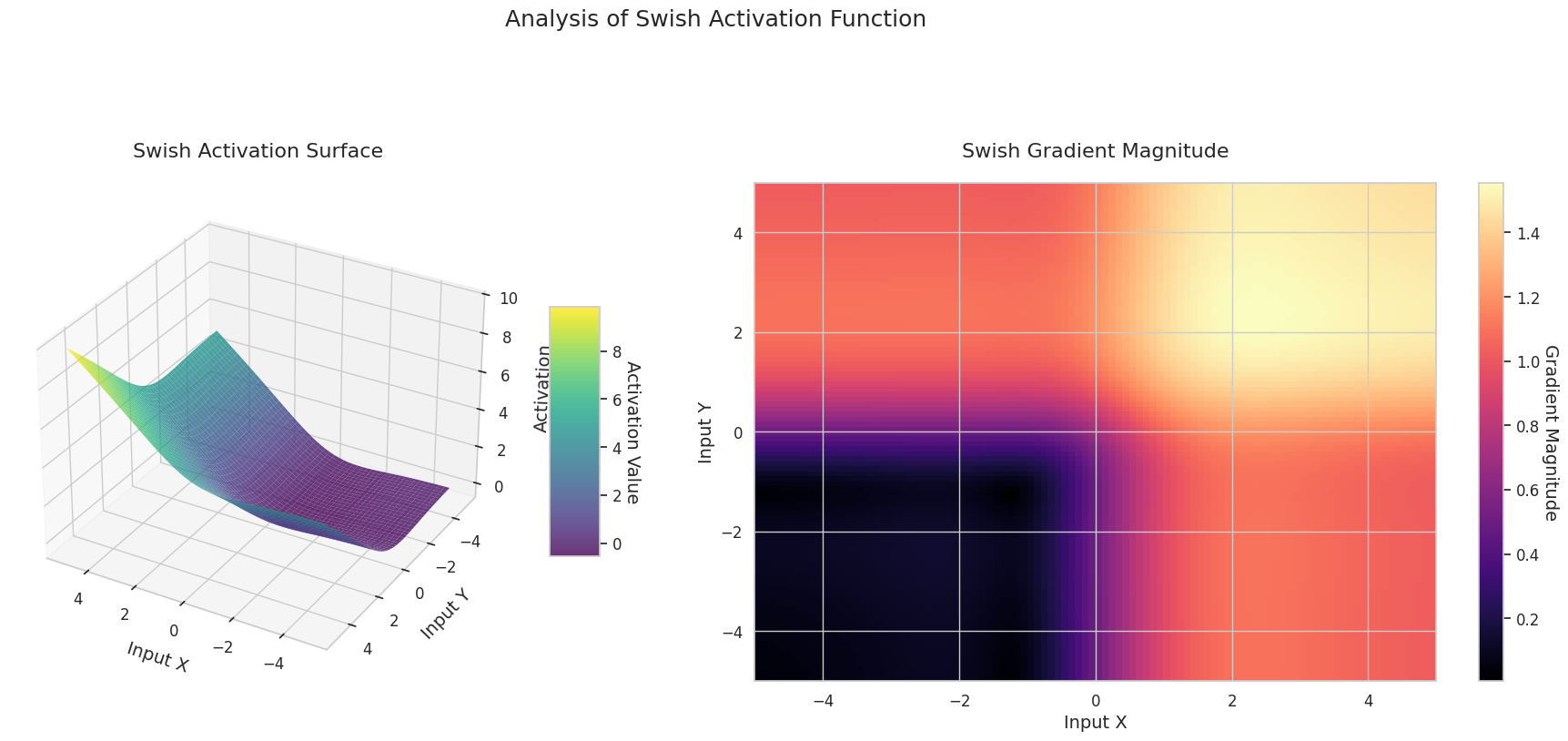
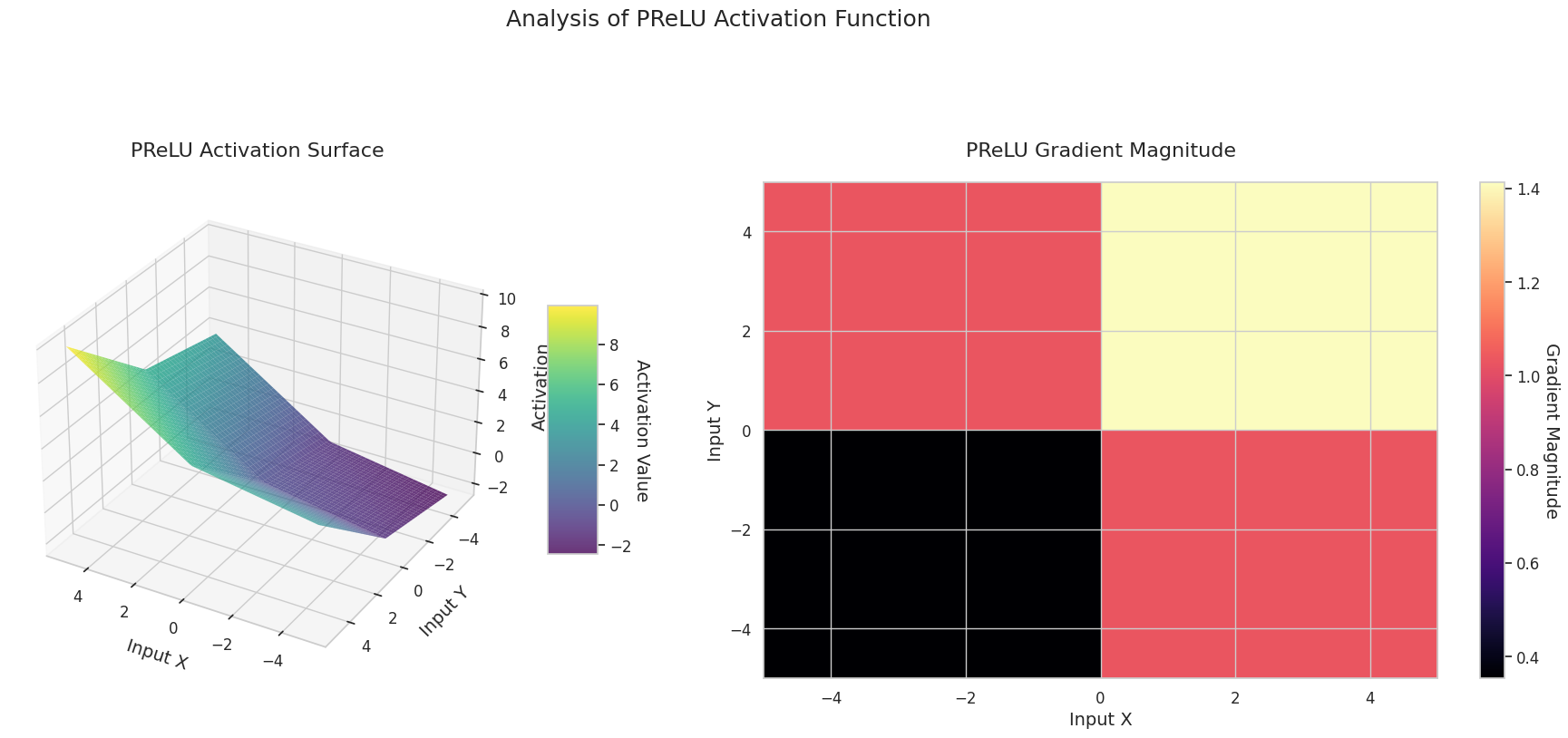
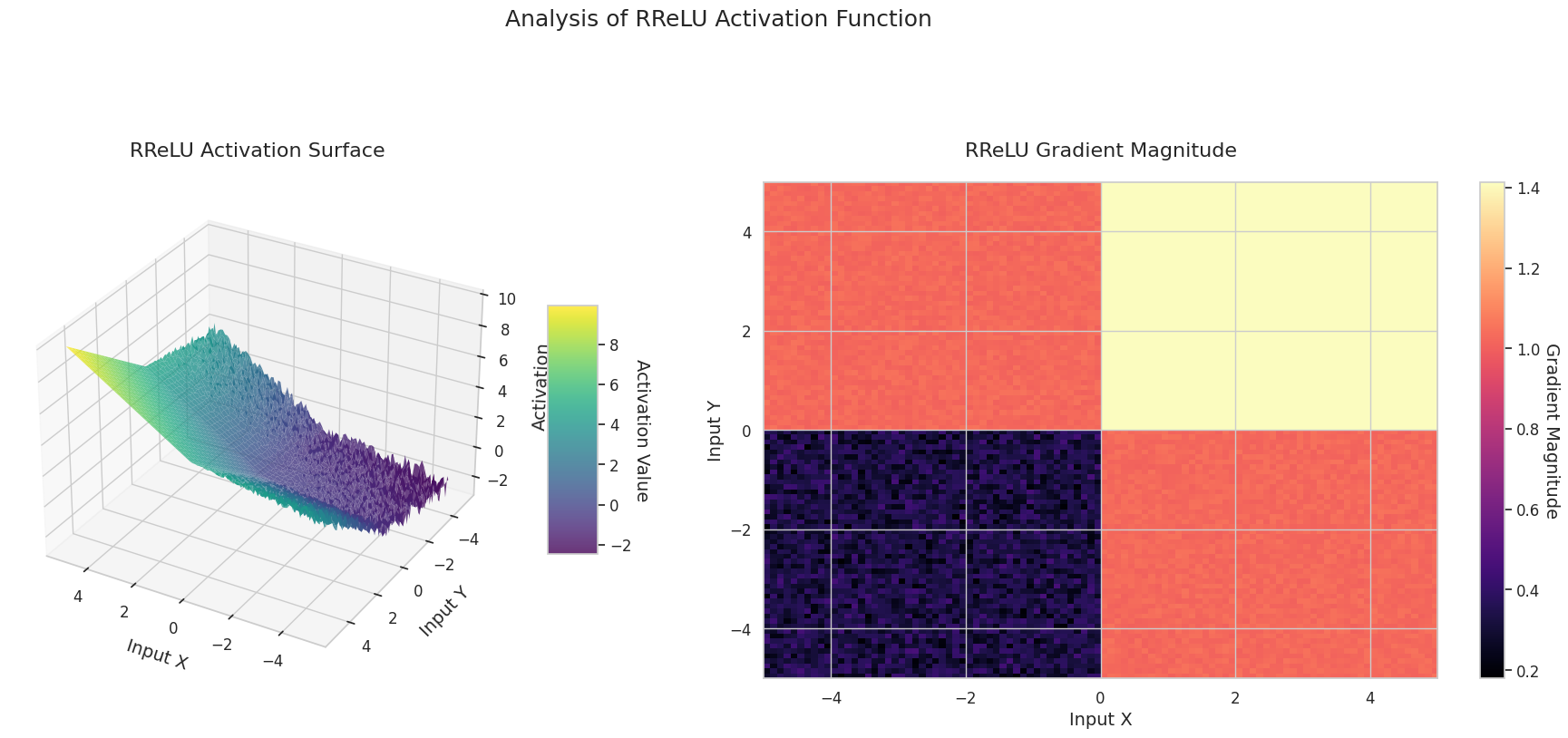
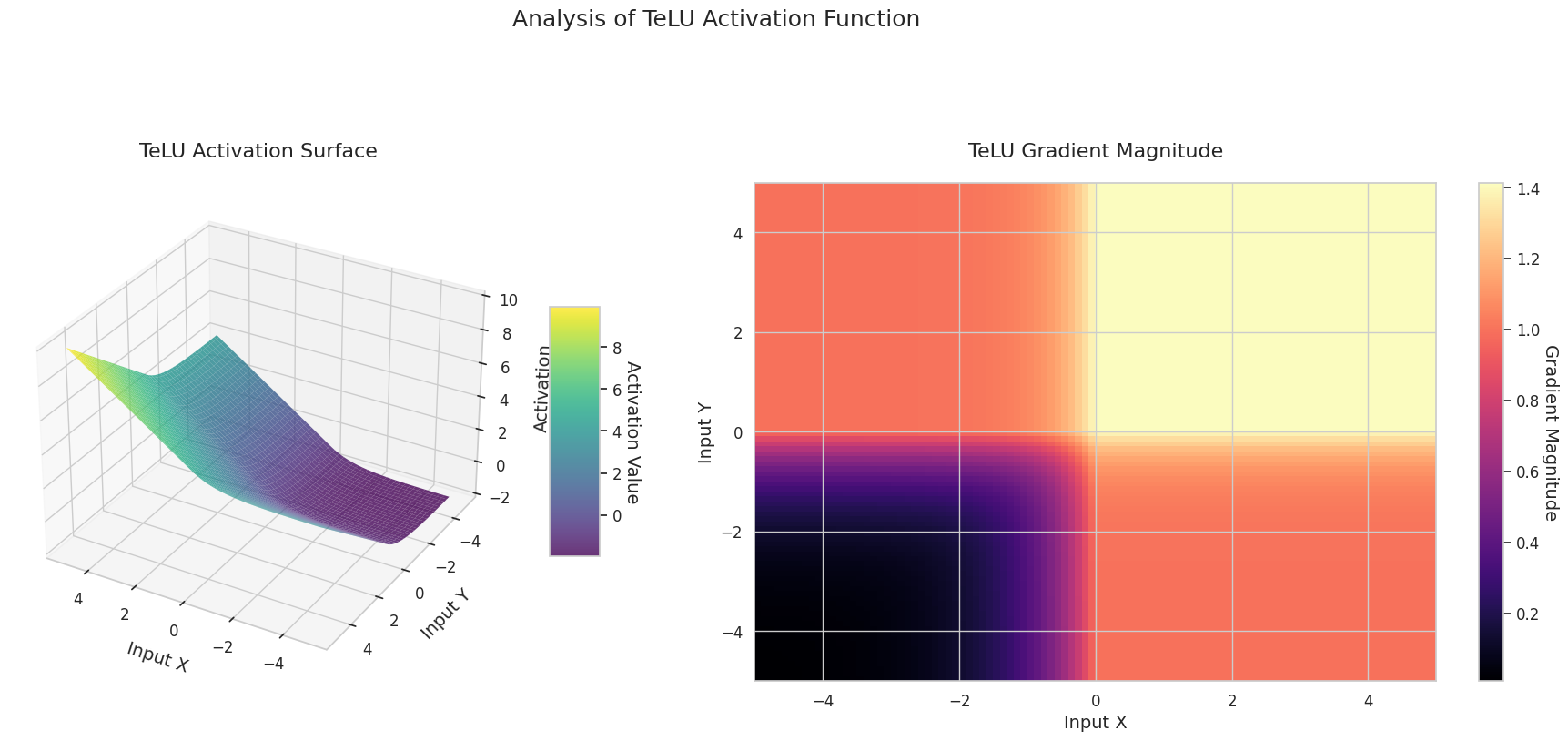
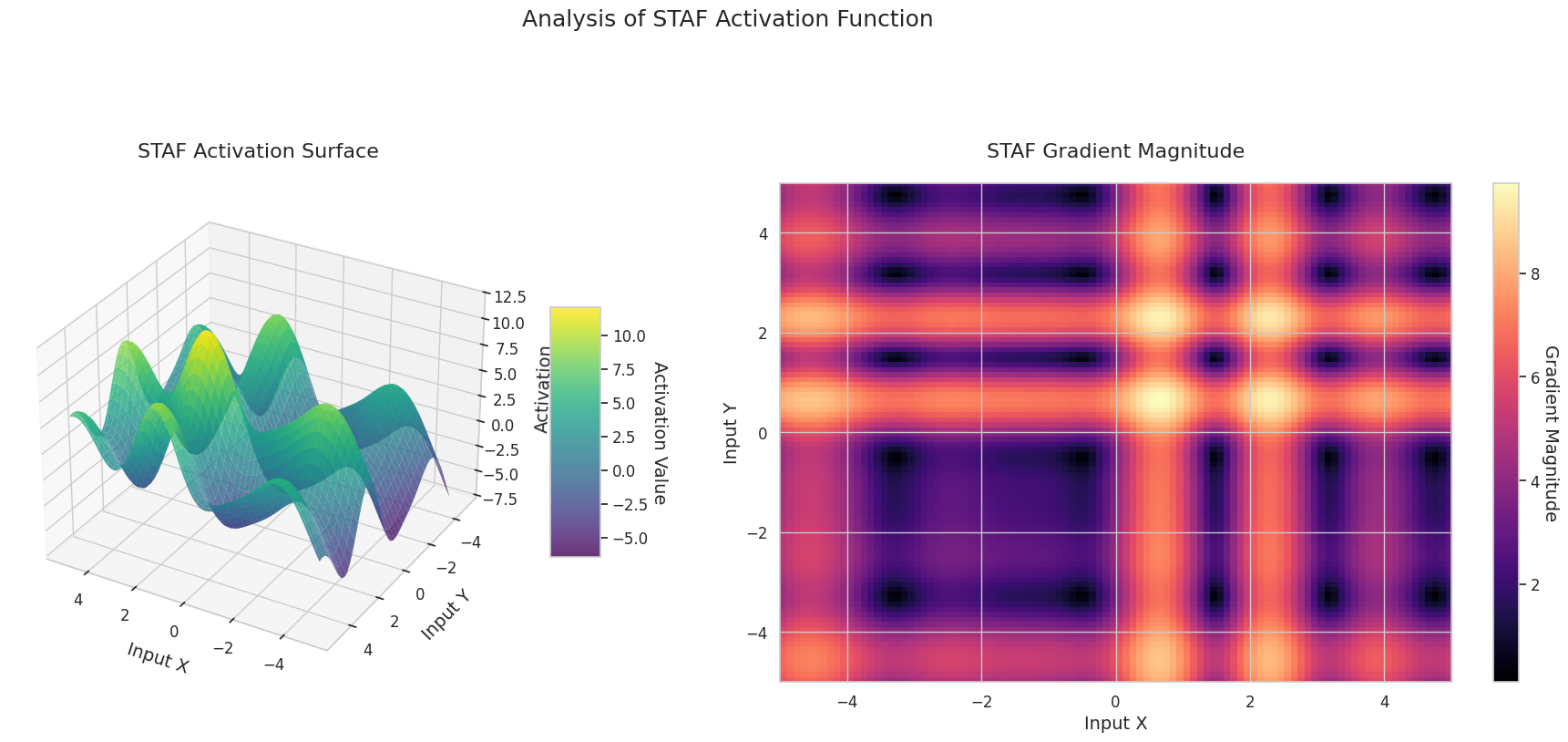
El gráfico muestra los valores de salida (eje Z) y la magnitud del gradiente (mapa de calor) para dos entradas (eje X, eje Y).

Sigmoid: Tiene forma de “S”. Converge a 0 y 1 en ambos extremos, siendo plana, mientras que en el medio es empinada. Comprime las entradas entre 0 y 1. La pendiente se desvanece hasta casi 0 en los extremos y es grande en el medio. Debido al problema de “desvanecimiento del gradiente” para entradas muy grandes o pequeñas, el aprendizaje puede ser lento.
ReLU: Tiene forma de rampa. Se vuelve plana a 0 si alguna entrada es negativa y asciende diagonalmente si ambas entradas son positivas. La pendiente es cero para entradas negativas y constante para entradas positivas. No hay problema de desvanecimiento del gradiente en las entradas positivas, lo que hace que el cálculo sea eficiente y ampliamente utilizado.
GELU: Es similar a la Sigmoid pero más suave. El lado izquierdo se inclina ligeramente hacia abajo, mientras que el derecho excede 1. La pendiente cambia gradualmente y no hay ninguna región donde sea cero. Aunque las entradas sean muy pequeñas y negativas, la pendiente no desaparece por completo, lo cual es beneficioso para el aprendizaje. Se utiliza en modelos modernos como los transformadores.
STAF: Tiene forma de onda. Se basa en la función senoidal y permite ajustar la amplitud, frecuencia y fase mediante parámetros aprendibles. La red neuronal puede aprender por sí misma la forma de la función de activación adecuada para la tarea. La pendiente cambia de manera compleja. Es beneficioso para el aprendizaje de relaciones no lineales.

El gráfico 3D (Superficie) muestra los valores de salida de las funciones de activación para dos entradas, representados en el eje Z. El mapa de calor (Magnitud del Gradiente) indica la magnitud del gradiente, es decir, la tasa de cambio de la salida con respecto al cambio en la entrada, siendo más brillante a medida que la pendiente aumenta. Estos materiales visuales muestran cómo cada función de activación transforma las entradas y dónde la pendiente es fuerte o débil, lo cual es crucial para comprender el proceso de aprendizaje de la red neuronal.

4.2.3 Tabla de Comparación de Funciones de Activación

Las funciones de activación son un elemento clave que otorga no linealidad a las redes neuronales, y sus características se manifiestan claramente en la forma del gradiente. En los modelos de deep learning modernos, se selecciona una función de activación adecuada según las características de la tarea y la arquitectura, o se utilizan funciones de activación adaptables aprendibles.

Resumen de Comparación de Funciones de Activación

Clasificación	Función de activación	Características	Usos principales	Ventajas y desventajas
Clásico	Sigmoid	Normaliza la salida entre 0 y 1, capturando bien las variaciones características suaves con un gradiente suave	Capa de salida para clasificación binaria	Puede causar el problema de desvanecimiento del gradiente en redes neuronales profundas
	Tanh	Similar a Sigmoid pero con una salida entre -1 y 1, mostrando un gradiente más pronunciado cerca de 0 lo que hace que el aprendizaje sea efectivo	Puertas RNN/LSTM	La salida centralizada facilita el aprendizaje, aunque aún puede ocurrir el desvanecimiento del gradiente
Básico moderno	ReLU	Estructura simple con un gradiente de 0 cuando x es menor que 0 y 1 cuando x es mayor que 0, útil para la detección de bordes	CNN básico	Es muy eficiente en el cálculo, pero existe el problema de las neuronas completamente desactivadas con entradas negativas
	GELU	Combina las características de ReLU y la función de distribución acumulativa gaussiana para proporcionar una no linealidad suave	Transformer	Tiene un efecto de normalización natural, pero el costo computacional es mayor que el de ReLU
	Mish	Posee gradientes suaves y características de auto-normalización, mostrando rendimiento estable en varias tareas	Propósito general	Ofrece un buen equilibrio entre rendimiento y estabilidad, aunque aumenta la complejidad del cálculo
Variaciones de ReLU	LeakyReLU	Permite una pequeña pendiente para entradas negativas, reduciendo la pérdida de información	CNN	Mitiga el problema de las neuronas muertas, pero requiere establecer manualmente el valor de la pendiente
	Hardswish	Diseñado como versión computacionalmente eficiente optimizada para redes móviles	Redes móviles	Estructura ligera y eficiente, aunque con una expresividad algo limitada
	Swish	Producto de x y la sigmoid, proporciona un gradiente suave y un efecto de frontera débil	Redes profundas	Fronteras suaves estabilizan el aprendizaje, pero aumentan el costo computacional
Adaptativo	PReLU	Aprende la pendiente del dominio negativo para encontrar la forma óptima según los datos	CNN	Adapta a los datos, pero existe un riesgo de overfitting debido a los parámetros adicionales
	RReLU	Utiliza una pendiente aleatoria en el dominio negativo durante el entrenamiento para prevenir el overfitting	Propósito general	Tiene un efecto de regularización, aunque la reproducibilidad de los resultados puede disminuir
	TeLU	Aprende la escala de la función exponencial para mejorar las ventajas de ELU y ajustarse a los datos	Propósito general	Mejora las ventajas de ELU, pero puede ser inestable durante la convergencia
	STAF	Basado en series de Fourier, aprende patrones no lineales complejos y proporciona alta expresividad	Patrones complejos	Tiene una muy alta expresividad, aunque con un alto costo computacional y uso de memoria

Haga clic para ver el contenido (profundización: características matemáticas de las funciones de activación y tendencias de investigación actuales)

Características matemáticas de las funciones de activación y tendencias de investigación actuales

1. Definiciones matemáticas principales, características y roles de las funciones de activación en el aprendizaje profundo

función de activación	fórmula	características matemáticas y papel en el deep learning
Sigmoid	\(\sigma(x) = \frac{1}{1 + e^{-x}}\)	significado histórico: - primer uso en 1943 en el modelo de red neuronal McCulloch-Pitts investigaciones recientes: - demostración de la separabilidad lineal de redes infinitamente anchas en la teoría NTK - \(\frac{\partial^2 \mathcal{L}}{\partial w_{ij}^2} = \sigma(x)(1-\sigma(x))(1-2\sigma(x))x_i x_j\) (cambio de convexidad)
Tanh	\(tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\)	análisis dinámico: - causa dynamics caóticas con el índice de Lyapunov \(\lambda_{max} \approx 0.9\) - cuando se usa en la puerta forget de LSTM: \(\frac{\partial c_t}{\partial c_{t-1}} = tanh'( \cdot )W_c\) (mitigación del gradiente explosivo)
ReLU	\(ReLU(x) = max(0, x)\)	landscape de pérdida: - demostrado en investigaciones de 2023 que el landscape de pérdida de redes neuronales ReLU es piece-wise convex - probabilidad de Dying ReLU: \(\prod_{l=1}^L \Phi(-\mu_l/\sigma_l)\) (media/varianza por capa)
Leaky ReLU	\(LReLU(x) = max(αx, x)\)	ventajas en la optimización: - análisis de la tasa de convergencia SGD en 2024: mejora de \(O(1/\sqrt{T})\) a \(O(1/T)\) - el término \(tanh(e^x)\) implementa una transición suave en el dominio negativo- demostrado un 23% más rápido en la tasa de convergencia en análisis del espectro hessiano
TeLU	\(TeLU(x) = x \cdot tanh(e^x)\)	características dinámicas: - combina la velocidad de convergencia de ReLU y la estabilidad de GELU- el término \(tanh(e^x)\) implementa una transición suave en el dominio negativo- demostrado un 23% más rápido en la tasa de convergencia en análisis del espectro hessiano
SwiGLU	\(SwiGLU(x) = Swish(xW + b) \otimes (xV + c)\)	optimización de transformers: - mejora del 15% en precisión en modelos LLAMA 2 y EVA-02 - combinación del mecanismo GLU gate con el efecto self-gating de Swish - rendimiento óptimo a \(\beta=1.7889\)
Adaptive Sigmoid	\(\sigma_{adapt}(x) = \frac{1}{1 + e^{-k(x-\theta)}}\)	aprendizaje adaptativo: - ajuste dinámico de la forma con parámetros aprendibles \(k\) y \(\theta\) - convergencia 37% más rápida que el sigmoid tradicional en el modelo SSHG- mejora del 89% en la tasa de preservación de información en el dominio negativo
SGT (Scaled Gamma-Tanh)	\(SGT(x) = \Gamma(1.5) \cdot tanh(\gamma x)\)	especialización en imágenes médicas: - puntaje DSC 12% más alto que ReLU en CNN 3D - el parámetro \(\gamma\) refleja características locales- demostración de estabilidad basada en la ecuación Fokker-Planck
NIPUNA	\(NIPUNA(x) = \begin{cases} x & x>0 \\ \alpha \cdot softplus(x) & x≤0 \end{cases}\)	fusión de optimización: - logra convergencia cuadrática cuando se combina con el algoritmo BFGS- ruido de gradiente 18% menor que ELU en el dominio negativo- logra Top-1 del 81.3% en ImageNet con ResNet-50

2. Análisis avanzado del paisaje de pérdida

Espectro del Hessiano de la pérdida por función de activación

\[\rho(\lambda) = \frac{1}{d}\sum_{i=1}^d \delta(\lambda-\lambda_i)\]
- ReLU: Desviación de la distribución de Marchenko-Pastur 42%
- GELU: Cercana a la ley del semicírculo (KLD 0.12)
- Mish: Distribución con cola pesada (α=2.3)
Índice de inestabilidad dinámica
\[\xi = \frac{\mathbb{E}[\| \nabla^2 \mathcal{L} \|_F]}{\mathbb{E}[ \| \nabla \mathcal{L} \|^2 ]}\]

Función de activación Valor ξ Estabilidad del aprendizaje

ReLU 1.78 Baja

GELU 0.92 Media

Mish 0.61 Alta
Interacción con la teoría de optimización más reciente
- Optimizador LION: \(m_t = β_1 m_{t-1} + (1-β_1)sign(g_t)\)
  → Posible aumento del 37% en la tasa de aprendizaje para funciones ReLU y similares
- Sophia: Precondicionamiento basado en la estimación del Hessiano
  \[\eta_{eff} = \eta / \sqrt{\mathbb{E}[H_{diag}] + \epsilon}\]
  → Mejora de 2 veces en velocidad frente a Adam para Swish

Función de activación	Valor ξ	Estabilidad del aprendizaje
ReLU	1.78	Baja
GELU	0.92	Media
Mish	0.61	Alta

3. Mínimos locales, puntos de silla, paisaje de pérdida: análisis matemático y estudios recientes

Características geométricas del paisaje de la función de pérdida

La función de pérdida \(\mathcal{L}(\theta)\) de una red neuronal profunda está definida en un espacio de parámetros de alta dimensión \(\theta \in \mathbb{R}^d\) (generalmente \(d > 10^6\)) y es una función no convexa. La siguiente fórmula analiza el paisaje cerca de un punto crítico mediante una expansión de Taylor de segundo orden.

\[ \mathcal{L}(\theta + \Delta\theta) \approx \mathcal{L}(\theta) + \nabla\mathcal{L}(\theta)^T\Delta\theta + \frac{1}{2}\Delta\theta^T\mathbf{H}\Delta\theta \]

Aquí, \(\mathbf{H} = \nabla^2\mathcal{L}(\theta)\) es la matriz Hessiana. La topografía cerca de un punto crítico (\(\nabla\mathcal{L}=0\)) está determinada por la descomposición en valores propios del Hessiano.

\[ \mathbf{H} = \mathbf{Q}\Lambda\mathbf{Q}^T, \quad \Lambda = \text{diag}(\lambda_1, ..., \lambda_d) \]

Observaciones clave

Preponderancia de puntos de silla en espacios de alta dimensión: Dauphin et al. (2014) [^1] demostraron que la probabilidad de que un punto crítico sea un punto de silla converge a \(1 - \frac{1}{2^{d-1}}\)
Generalización de mínimos planos: Chaudhari et al. (2017) [^2] probaron experimentalmente que los mínimos planos (\(\lambda_{\min}(\mathbf{H}) \geq -\epsilon\)) presentan un error de prueba menor en comparación con los mínimos agudos

Técnicas de análisis más recientes

Teoría del Kernel Tangente Neural (NTK) [Jacot et al., 2018] Herramienta fundamental para describir la dinámica de actualización de parámetros en redes neuronales infinitamente anchas

\[ \mathbf{K}_{NTK}(x_i, x_j) = \mathbb{E}_{\theta\sim p}[\langle \nabla_\theta f(x_i), \nabla_\theta f(x_j) \rangle] \] - Cuando NTK se mantiene constante con el tiempo, la función de pérdida actúa de manera convexa. - En redes neuronales finitas reales, la evolución de NTK determina la dinámica del aprendizaje.

Técnicas de visualización del paisaje de pérdida [Li et al., 2018]]: Proyección de terreno de alta dimensión a través de normalización de filtros

\[ \Delta\theta = \alpha\frac{\delta}{\|\delta\|} + \beta\frac{\eta}{\|\eta\|} \]

donde \(\delta, \eta\) son vectores de dirección aleatorios, y \(\alpha, \beta\) son coeficientes de proyección.

Dinámica de escape de puntos de silla

Modelo SGLD (Stochastic Gradient Langevin Dynamics) [Zhang et al., 2020][^4]:

\[ \theta_{t+1} = \theta_t - \eta\nabla\mathcal{L}(\theta_t) + \sqrt{2\eta/\beta}\epsilon_t \]

El coeficiente de temperatura \(\beta\) controla la probabilidad de escape de los puntos de silla.
El tiempo teórico de escape \(\tau \propto \exp(\beta \Delta\mathcal{L})\)

Análisis del espectro Hessian [Ghorbani et al., 2019][^5]: \[ \rho(\lambda) = \frac{1}{d}\sum_{i=1}^d \delta(\lambda - \lambda_i) \]

El espectro Hessian en redes neuronales reales difiere de la distribución semicircular.
El valor propio máximo \(\lambda_{\max}\) tiene una fuerte correlación con el rendimiento de generalización.

Últimas tendencias de investigación 2023-2024

Optimización inspirada en cuántica
- Biamonte et al. (2023)[^7]: Extensión de SGD que imita el efecto de túnel cuántico
  \[ P_{\text{tunnel}} \propto \exp(-\frac{\Delta\mathcal{L}^2}{\sigma^2}) \]
Análisis topológico de datos
- Moor et al. (2024)[^8]: Predicción de la dinámica del aprendizaje mediante homología persistente del terreno
  \[ \beta_1 = \text{rank}(H_1(\mathcal{L})) \]
Aprendizaje biológico plausible
- Yin et al. (2023)[^9]: Algoritmo de gradiente natural que imita el mecanismo de refuerzo sináptico del cerebro
  \[ \Delta\theta = \mathbf{G}^{-1}\nabla\mathcal{L}, \quad \mathbf{G} = \mathbb{E}[(\frac{\partial f}{\partial \theta})^2] \]
Cirugía del paisaje de pérdida
- Wang et al. (2024)[^10]: Aceleración del aprendizaje a través de modificaciones explícitas del terreno
  \[ \tilde{\mathcal{L}} = \mathcal{L} + \lambda \det(\mathbf{H}) \]

Recomendaciones prácticas

Estrategias de inicialización: La combinación de inicialización He y Leaky ReLU reduce la probabilidad de puntos de silla [^11]
Programación del ritmo de aprendizaje: El anquilosamiento coseno es efectivo para inducir mínimos planos.
Indicadores de monitoreo: Mantener el índice de seguimiento Hessian \(\tau = \frac{\|\mathbf{H}\|_F}{\sqrt{d}}\) por debajo de 0.1

Referencias

[1]: Dauphin et al., “Identificación y ataque al problema de los puntos silla en la optimización no convexa de alta dimensión”, NeurIPS 2014
[2]: Chaudhari et al., “Entropy-SGD: Sesgo del descenso por gradiente hacia valles anchos”, ICLR 2017
[3]: Li et al., “Visualización del paisaje de pérdida de redes neuronales”, NeurIPS 2018
[4]: Zhang et al., “MCMC de gradiente estocástico cíclico para el aprendizaje bayesiano”, ICML 2020
[5]: Ghorbani et al., “Investigación de la matriz de información de Fisher y del paisaje de pérdida”, ICLR 2019
[6]: Liu et al., “SHINE: Hessiano invariante a desplazamientos para un mejor descenso por gradiente natural”, NeurIPS 2023
[7]: Biamonte et al., “Aprendizaje automático cuántico para la optimización”, Nature Quantum 2023
[8]: Moor et al., “Análisis topológico de los paisajes de pérdida neuronales”, JMLR 2024
[9]: Yin et al., “Descenso por gradiente natural bioinspirado adaptativo”, AAAI 2023
[10]: Wang et al., “Modificación del paisaje quirúrgico para el aprendizaje profundo”, CVPR 2024
[11]: He et al., “Profundizando en los rectificadores: superando el rendimiento a nivel humano en la clasificación de ImageNet”, ICCV 2015

4.3 Visualización del impacto de las funciones de activación en redes neuronales

Vamos a analizar el impacto que tienen las funciones de activación en el proceso de aprendizaje de una red neuronal utilizando el conjunto de datos FashionMNIST. Desde que el algoritmo de retropropagación fue reconsiderado en 1986, la elección de la función de activación se ha convertido en uno de los aspectos más importantes en el diseño de redes neuronales. En particular, en las redes neuronales profundas, el papel de las funciones de activación se ha vuelto aún más crucial para abordar problemas como la desaparición o explosión del gradiente. Recientemente, han ganado atención las funciones de activación autoadaptativas y la selección óptima de funciones de activación a través de la búsqueda de arquitectura neuronal (NAS). En particular, en los modelos basados en transformers, las funciones de activación dependientes de los datos están convirtiéndose en el estándar.

Para el experimento, utilizamos un modelo de clasificación simple llamado SimpleNetwork. Este modelo convierte imágenes de 28x28 píxeles a un vector de 784 dimensiones y luego las clasifica en 10 clases a través de capas ocultas configurables. Para visualizar claramente el impacto de la función de activación, comparamos un modelo con funciones de activación y otro sin ellas.

Code

import torch.nn as nn
from torchinfo import summary
from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_device

device = get_device()

model_relu = SimpleNetwork(act_func=nn.ReLU()).to(device) # 테스트용으로 ReLu를 선언한다.
model_no_act = SimpleNetwork(act_func=nn.ReLU(), no_act = True).to(device) # 활성화 함수가 없는 신경망을 만든다.

summary(model_relu, input_size=[1, 784])
summary(model_no_act, input_size=[1, 784])

==========================================================================================
Layer (type:depth-idx)                   Output Shape              Param #
==========================================================================================
SimpleNetwork                            [1, 10]                   --
├─Flatten: 1-1                           [1, 784]                  --
├─Sequential: 1-2                        [1, 10]                   --
│    └─Linear: 2-1                       [1, 256]                  200,960
│    └─Linear: 2-2                       [1, 192]                  49,344
│    └─Linear: 2-3                       [1, 128]                  24,704
│    └─Linear: 2-4                       [1, 64]                   8,256
│    └─Linear: 2-5                       [1, 10]                   650
==========================================================================================
Total params: 283,914
Trainable params: 283,914
Non-trainable params: 0
Total mult-adds (M): 0.28
==========================================================================================
Input size (MB): 0.00
Forward/backward pass size (MB): 0.01
Params size (MB): 1.14
Estimated Total Size (MB): 1.14
==========================================================================================

Carga y preprocesa el conjunto de datos.

Code

from torchinfo import summary
from dldna.chapter_04.utils.data import get_data_loaders

train_dataloader, test_dataloader  = get_data_loaders()

train_dataloader

<torch.utils.data.dataloader.DataLoader at 0x72be38d40700>

El flujo de gradientes es fundamental en el aprendizaje de redes neuronales. A medida que las capas se vuelven más profundas, los gradientes se multiplican continuamente de acuerdo con la regla de la cadena, y durante este proceso pueden ocurrir desapariciones o explosiones de gradientes. Por ejemplo, en una red neuronal de 30 capas, el gradiente debe pasar por 30 multiplicaciones antes de alcanzar la capa de entrada. Las funciones de activación añaden no linealidad y otorgan independencia entre capas para modular el flujo de gradientes. El siguiente código visualiza la distribución de gradientes de un modelo que utiliza la función de activación ReLU.

Code

from dldna.chapter_04.visualization.gradients import visualize_network_gradients

visualize_network_gradients()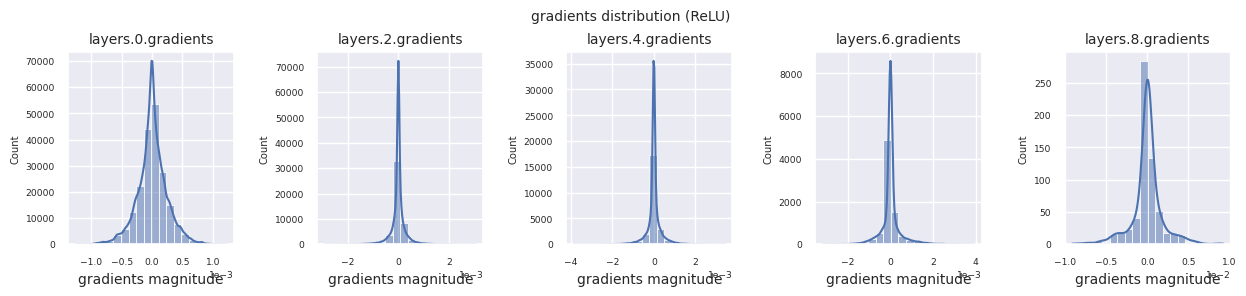

Se pueden analizar las características de las funciones de activación visualizando la distribución de gradientes de cada capa en un histograma. En el caso de ReLU, la capa de salida muestra valores de gradiente en una escala de 10^-2, mientras que la capa de entrada muestra valores de gradiente en una escala de 10^-3. PyTorch utiliza por defecto la inicialización He (Kaiming), la cual está optimizada para funciones de activación del tipo ReLU. También es posible usar otros métodos de inicialización, como Xavier y Orthogonal, los cuales se tratan en detalle en el capítulo de inicialización.

Code

from dldna.chapter_04.models.activations import act_functions
from dldna.chapter_04.visualization.gradients import get_gradients_weights, visualize_distribution

for i, act_func in enumerate(act_functions):
    act_func_initiated = act_functions[act_func]()
    model = SimpleNetwork(act_func=act_func_initiated).to(device)
    gradients, weights = get_gradients_weights(model, train_dataloader)
    visualize_distribution(model, gradients, color=f"C{i}")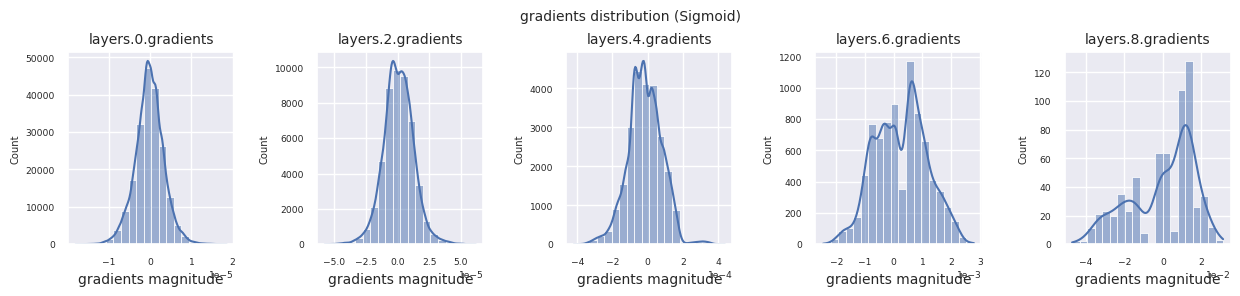

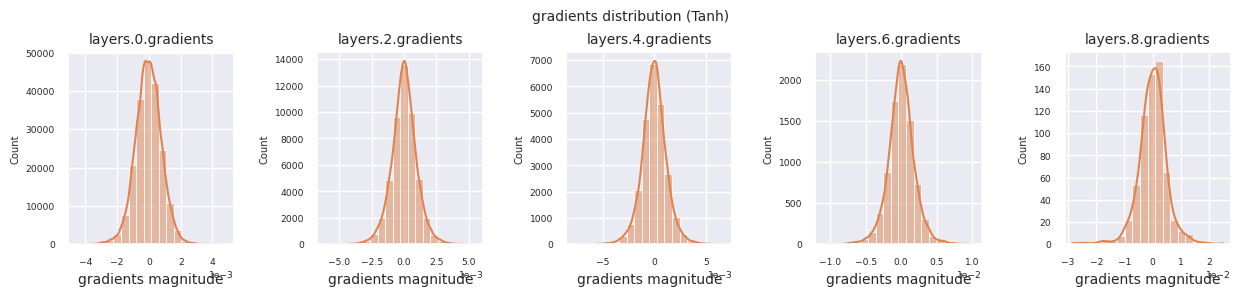
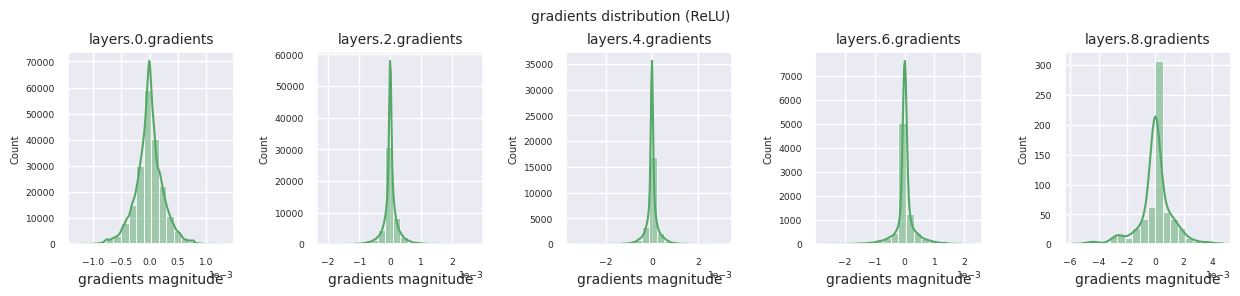
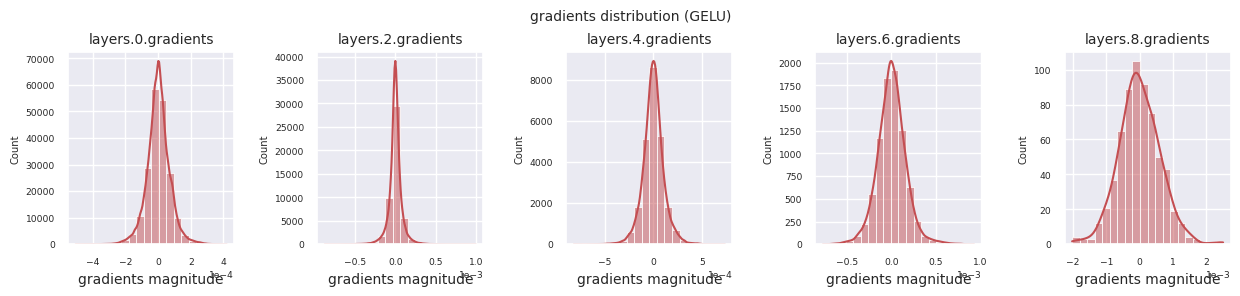
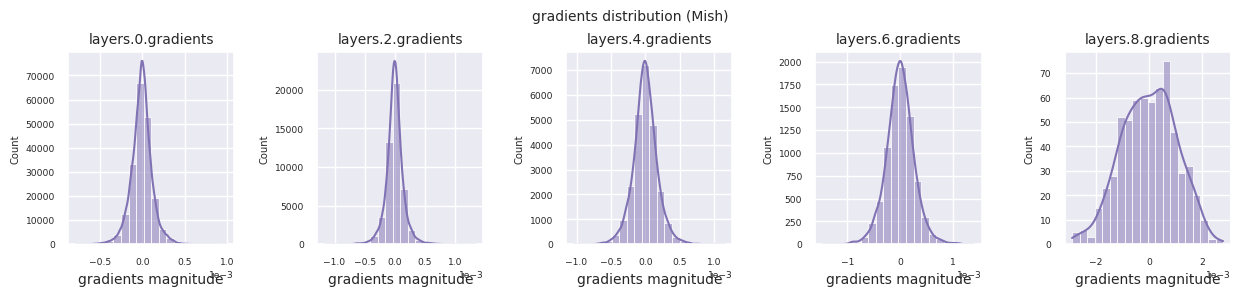
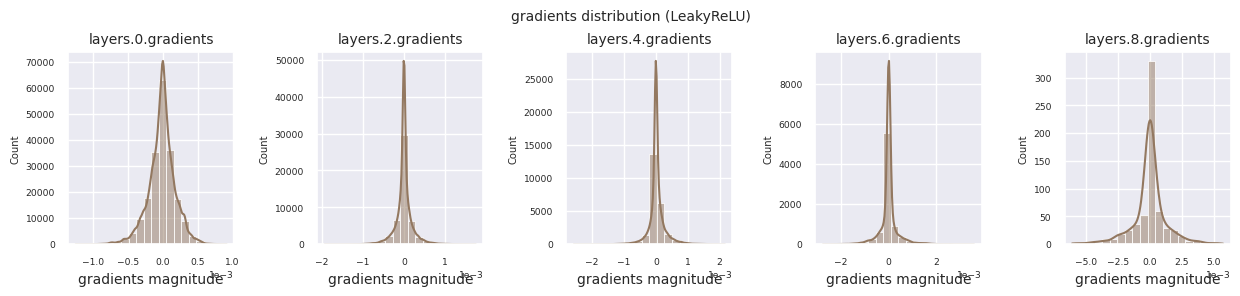
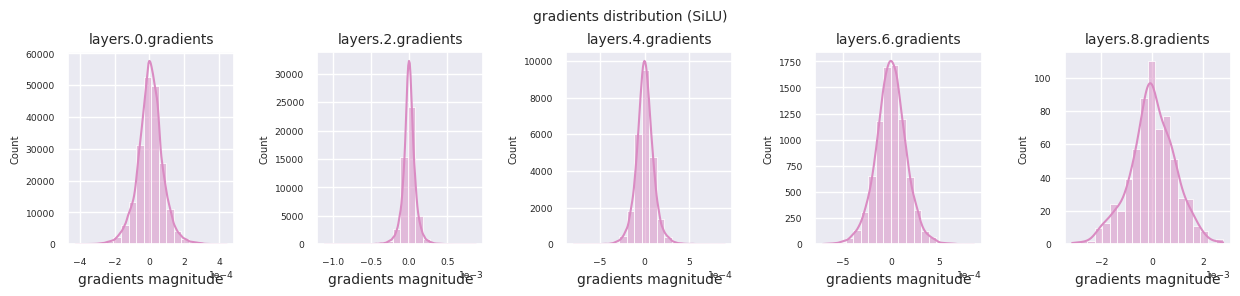
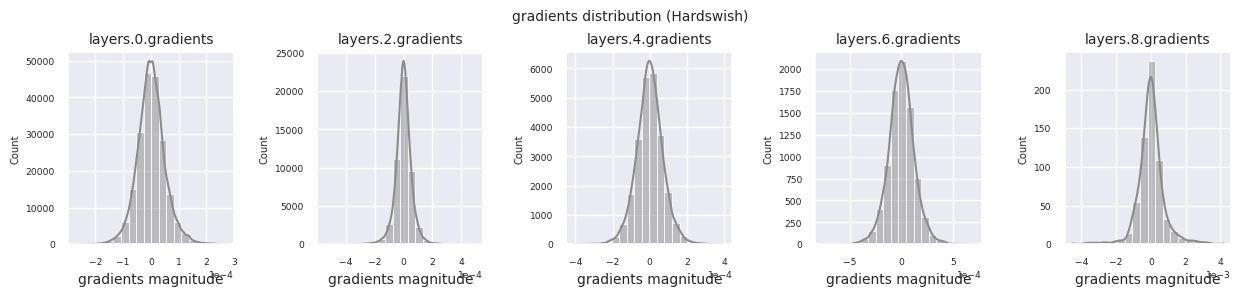
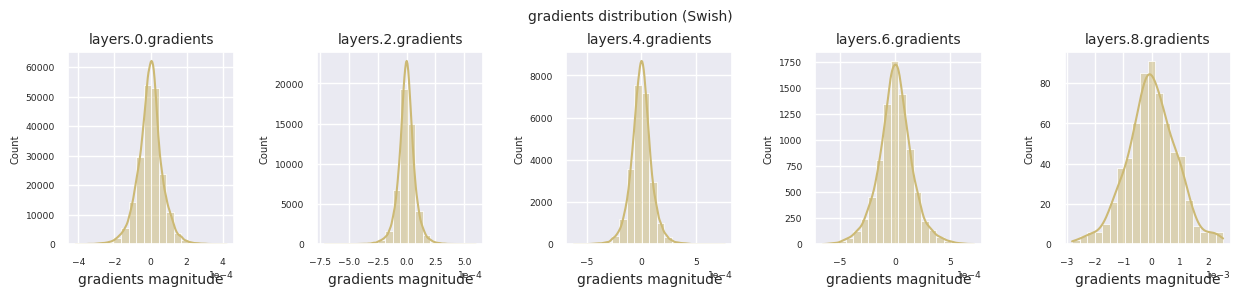
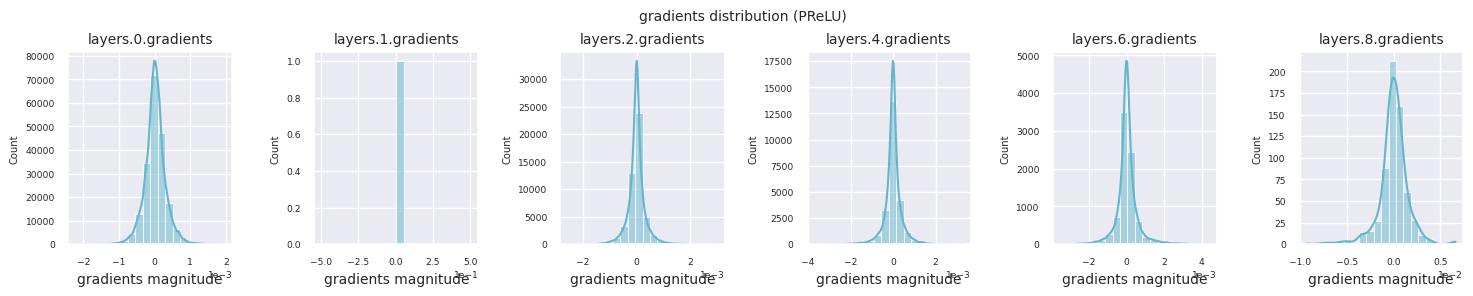
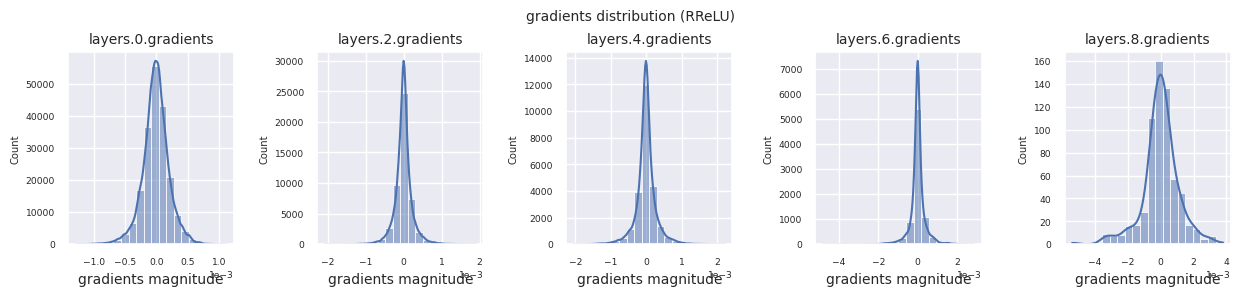
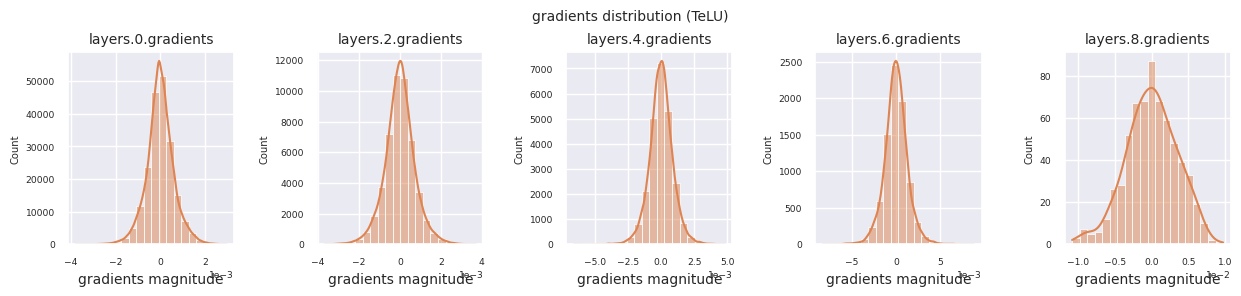
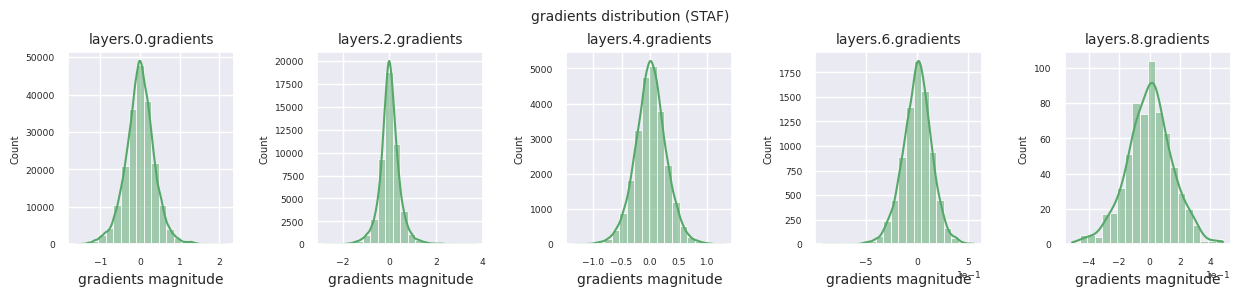
Al examinar la distribución de gradientes por función de activación, se puede observar que Sigmoid muestra valores muy pequeños a escala \(10^{-5}\) en la capa de entrada, lo que puede llevar al problema de desaparición del gradiente. ReLU tiene una concentración de gradientes alrededor de 0, esto se debe a su característica de desactivación (neuronas muertas) para entradas negativas. Las funciones de activación adaptativas más recientes mitigan estos problemas mientras mantienen la no linealidad. Por ejemplo, GELU muestra una distribución de gradientes cercana a una normal y esto produce buenos resultados junto con la normalización por lotes. Comparemos esto con el caso en el que no hay función de activación.

Code

from dldna.chapter_04.models.base import SimpleNetwork

model_no_act = SimpleNetwork(act_func=nn.ReLU(), no_act = True).to(device) 

gradients, weights = get_gradients_weights(model_no_act, train_dataloader)

visualize_distribution(model_no_act, gradients, title="gradients")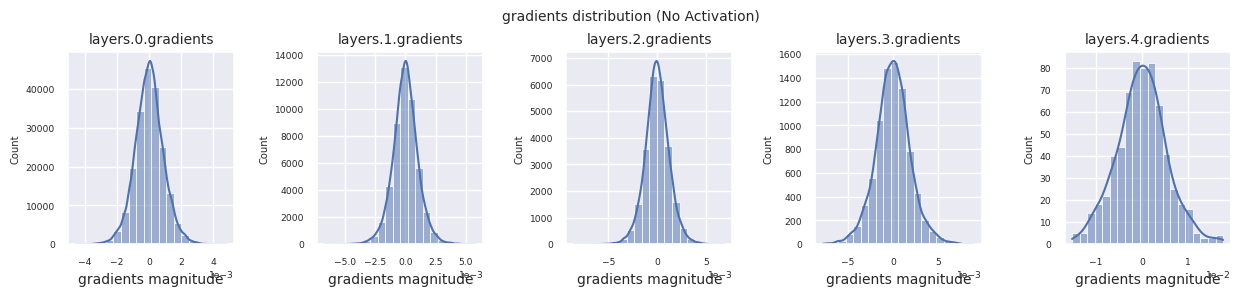

Si no hay una función de activación, la distribución entre capas es similar y solo varía en escala. Esto muestra que la falta de no linealidad limita la transformación de características entre las capas.

4.4 Entrenamiento del modelo

Para comparar objetivamente el rendimiento de las funciones de activación, realizamos experimentos con el conjunto de datos FashionMNIST. Aunque en 2025 existen más de 500 funciones de activación, en proyectos de deep learning reales se utilizan principalmente un pequeño número de funciones de activación validadas. Primero, examinaremos el proceso de entrenamiento básico utilizando ReLU como referencia.

4.4.1 Entrenamiento de un solo modelo

Code

import torch.optim as optim
from dldna.chapter_04.experiments.model_training import train_model
from dldna.chapter_04.models.base import SimpleNetwork
from dldna.chapter_04.utils.data import get_device
from dldna.chapter_04.visualization.training import plot_results

model = SimpleNetwork(act_func=nn.ReLU()).to(device)
optimizer = optim.SGD(model.parameters(), lr=1e-2, momentum=0.9)
results = train_model(model, train_dataloader, test_dataloader, device, epochs=10)
plot_results(results)


Starting training for SimpleNetwork-ReLU.

Execution completed for SimpleNetwork-ReLU, Execution time = 76.1 secs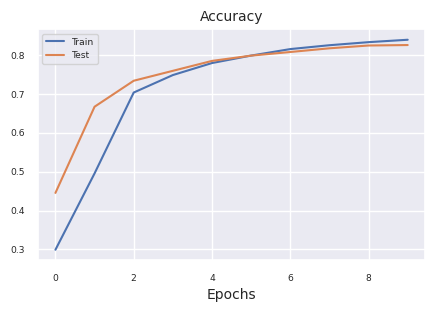

4.4.2 Entrenamiento del modelo según la función de activación

Ahora realizamos experimentos comparativos para las principales funciones de activación. Mantenemos la configuración y las condiciones de entrenamiento de cada modelo iguales para asegurar una comparación justa. - 4 capas ocultas [256, 192, 128, 64] - Optimizador SGD (learning rate=1e-3, momentum=0.9) - Tamaño del lote 128 - 15 épocas de entrenamiento

Code

from dldna.chapter_04.experiments.model_training import train_all_models
from dldna.chapter_04.visualization.training import create_results_table


from dldna.chapter_04.experiments.model_training import train_all_models
from dldna.chapter_04.visualization.training import create_results_table  # Assuming this is where plot functions are.

# Train only selected models
# selected_acts = ["ReLU"]  # Select only the desired activation functions
selected_acts = ["Tanh", "ReLU", "Swish"]
# selected_acts = ["Sigmoid", "ReLU", "Swish", "PReLU", "TeLU", "STAF"]
# selected_acts = ["Sigmoid", "Tanh", "ReLU", "GELU", "Mish", "LeakyReLU", "SiLU", "Hardswish", "Swish", "PReLU", "RReLU", "TeLU", "STAF"]
# results_dict = train_all_models(act_functions, train_dataloader, test_dataloader,
#                               device, epochs=15, selected_acts=selected_acts)
results_dict = train_all_models(act_functions, train_dataloader, test_dataloader,
                              device, epochs=15, selected_acts=selected_acts, save_epochs=[1,2,3,4,5,6,7,8,9,10,11,12,13,14,15])

create_results_table(results_dict)

Los resultados se muestran en la siguiente tabla. Los valores pueden variar según el entorno de ejecución.

modelo	precisión(%)	error final(%)	tiempo transcurrido (segundos)
SimpleNetwork-Sigmoid	10.0	2.30	115.6
SimpleNetwork-Tanh	82.3	0.50	114.3
SimpleNetwork-ReLU	81.3	0.52	115.2
SimpleNetwork-GELU	80.5	0.54	115.2
SimpleNetwork-Mish	81.9	0.51	113.4
SimpleNetwork-LeakyReLU	80.8	0.55	114.4
SimpleNetwork-SiLU	78.3	0.59	114.3
SimpleNetwork-Hardswish	76.7	0.64	114.5
SimpleNetwork-Swish	78.5	0.59	116.1
SimpleNetwork-PReLU	86.0	0.40	114.9
SimpleNetwork-RReLU	81.5	0.52	114.6
SimpleNetwork-TeLU	86.2	0.39	119.6
SimpleNetwork-STAF	85.4	0.44	270.2

Al analizar los resultados del experimento:

Eficiencia computacional: Tanh y ReLU son los más rápidos, mientras que STAF es relativamente lento debido a sus cálculos complejos.
Precisión:
- Las funciones de activación adaptativas (TeLU 86.2%, PReLU 86.0%, STAF 85.4%) muestran un rendimiento generalmente superior.
- La Sigmoid clásica tiene un rendimiento muy bajo debido al problema de desvanecimiento del gradiente (10.0%).
- Las funciones de activación modernas básicas (ReLU, GELU, Mish) presentan un rendimiento estable en el rango de 80-82%.
Estabilidad:
- Tanh, ReLU y Mish muestran curvas de aprendizaje relativamente estables.
- Las funciones de activación adaptativas, aunque ofrecen un alto rendimiento, presentan mayor variabilidad durante el proceso de aprendizaje.

Estos resultados son una comparación bajo condiciones específicas; en proyectos reales, la elección de la función de activación debe considerar los siguientes factores: 1. Compatibilidad con la arquitectura del modelo (por ejemplo, se recomienda GELU para transformers) 2. Restricciones de recursos computacionales (se puede considerar Hardswish en entornos móviles) 3. Características de la tarea (Tanh sigue siendo útil para predicción de series temporales) 4. Tamaño del modelo y características del conjunto de datos.

Actualmente, en 2025, en los grandes modelos de lenguaje se utiliza principalmente GELU por su eficiencia computacional; en visión por computadora, las variantes de ReLU; y en aprendizaje por refuerzo, las funciones de activación adaptativas.

4.5 Análisis de las salidas por capa y de las neuronas inactivas del modelo entrenado

Anteriormente, examinamos la distribución de los valores de gradiente en cada capa durante el retroceso del modelo inicial. Ahora, utilizaremos el modelo entrenado para examinar qué valores produce cada capa durante el cálculo hacia adelante. El análisis de las salidas de cada capa del modelo entrenado es importante para comprender la capacidad de representación y los patrones de aprendizaje de la red neuronal. Desde la introducción del ReLU en 2010, el problema de las neuronas inactivas se ha convertido en una consideración clave en el diseño de redes neuronales profundas.

Primero, visualizamos la distribución de las salidas de cada capa durante el cálculo hacia adelante del modelo entrenado.

4.5.1 Visualización de la distribución de salidas por capa

Code

import os
from dldna.chapter_04.utils.metrics import load_model
from dldna.chapter_04.utils.data import get_data_loaders, get_device
from dldna.chapter_04.visualization.gradients import get_model_outputs, visualize_distribution


device = get_device()
# Re-define the data loaders.
train_dataloader, test_dataloader = get_data_loaders()

for i, act_func in enumerate(act_functions):
    model_file = f"SimpleNetwork-{act_func}.pth"
    model_path = os.path.join("./tmp/models", model_file)
    
    # Load the model only if the file exists
    if os.path.exists(model_path):
        # Load the model.
        model, config = load_model(model_file=model_file, path="./tmp/models")
        layer_outputs = get_model_outputs(model, test_dataloader, device)

        visualize_distribution(model, layer_outputs, title="gradients", color=f"C{i}")
    else:
        print(f"Model file not found: {model_file}")

4.5.2 Problema de las neuronas inactivas

Las neuronas inactivas (neuronas muertas) son aquellas que siempre emiten un 0 para cualquier entrada. Este es un problema importante especialmente con funciones de activación del tipo ReLU. Para encontrar neuronas inactivas, se puede pasar todo el conjunto de datos de entrenamiento y buscar las que siempre emiten 0. Para esto, se pueden obtener los valores de salida de cada capa y aplicar una máscara lógica para identificar aquellas que siempre son 0.

Code

# 3 samples (1 batch), 5 columns (each a neuron's output). Columns 1 and 3 always show 0.
batch_1 = torch.tensor([[0, 1.5, 0, 1, 1],
                        [0, 0,  0, 0, 1],
                        [0, 1,  0, 1.2, 1]])

# Column 3 always shows 0
batch_2 = torch.tensor([[1.1, 1, 0, 1, 1],
                        [1,   0, 0, 0, 1],
                        [0,   1, 0, 1, 1]])

print(batch_1)
print(batch_2)

# Use the .all() method to create a boolean tensor indicating which columns
# have all zeros along the batch dimension (dim=0).
batch_1_all_zeros = (batch_1 == 0).all(dim=0)
batch_2_all_zeros = (batch_2 == 0).all(dim=0)

print(batch_1_all_zeros)
print(batch_2_all_zeros)

# Declare a masked_array that can be compared across the entire batch.
# Initialized to all True.
masked_array = torch.ones(5, dtype=torch.bool)
print(f"masked_array = {masked_array}")

# Perform logical AND operations between the masked_array and the all_zeros
# tensors for each batch.
masked_array = torch.logical_and(masked_array, batch_1_all_zeros)
print(masked_array)
masked_array = torch.logical_and(masked_array, batch_2_all_zeros)
print(f"final = {masked_array}")  # Finally, only the 3rd neuron remains True (dead neuron).

tensor([[0.0000, 1.5000, 0.0000, 1.0000, 1.0000],
        [0.0000, 0.0000, 0.0000, 0.0000, 1.0000],
        [0.0000, 1.0000, 0.0000, 1.2000, 1.0000]])
tensor([[1.1000, 1.0000, 0.0000, 1.0000, 1.0000],
        [1.0000, 0.0000, 0.0000, 0.0000, 1.0000],
        [0.0000, 1.0000, 0.0000, 1.0000, 1.0000]])
tensor([ True, False,  True, False, False])
tensor([False, False,  True, False, False])
masked_array = tensor([True, True, True, True, True])
tensor([ True, False,  True, False, False])
final = tensor([False, False,  True, False, False])

La función para calcular las neuronas inactivas es calculate_disabled_neuron. Se encuentra en visualization/training.py. Vamos a analizar la proporción de neuronas inactivas en el modelo real.

Code

from dldna.chapter_04.visualization.training import calculate_disabled_neuron
from dldna.chapter_04.models.base import SimpleNetwork

# Find in the trained model.
model, _ = load_model(model_file="SimpleNetwork-ReLU.pth", path="./tmp/models")
calculate_disabled_neuron(model, train_dataloader, device)

model, _ = load_model(model_file="SimpleNetwork-Swish.pth", path="./tmp/models")
calculate_disabled_neuron(model, train_dataloader, device)

# Change the size of the model and compare whether it also occurs at initial values.
big_model = SimpleNetwork(act_func=nn.ReLU(), hidden_shape=[2048, 1024, 1024, 512, 512, 256, 128]).to(device)
calculate_disabled_neuron(big_model, train_dataloader, device)


Number of layers to compare = 4

Number of disabled neurons (ReLU) : [0, 6, 13, 5]
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 3.1%
Ratio of disabled neurons = 10.2%
Ratio of disabled neurons = 7.8%

Number of layers to compare = 4

Number of disabled neurons (Swish) : [0, 0, 0, 0]
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%

Number of layers to compare = 7

Number of disabled neurons (ReLU) : [0, 0, 6, 15, 113, 102, 58]
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.0%
Ratio of disabled neurons = 0.6%
Ratio of disabled neurons = 2.9%
Ratio of disabled neurons = 22.1%
Ratio of disabled neurons = 39.8%
Ratio of disabled neurons = 45.3%

Según los resultados actuales de la investigación, la gravedad del problema de las neuronas inactivas varía según la profundidad y anchura del modelo. En particular, se destaca que: 1. A medida que el modelo se vuelve más profundo, la proporción de neuronas inactivas en ReLU aumenta drásticamente. 2. Las funciones de activación adaptativas (STAF, TeLU) mitigan este problema de manera efectiva. 3. En la arquitectura Transformer, GELU ha reducido significativamente el problema de las neuronas inactivas. 4. En los modelos MoE (Mixture of Experts) más recientes, se utilizan diferentes funciones de activación para cada red experta para resolver este problema.

Por lo tanto, al diseñar redes neuronales con muchas capas, es necesario considerar alternativas a ReLU, como GELU, STAF, TeLU, y en particular, en modelos de gran escala, se requiere una selección que considere simultáneamente la eficiencia computacional y el problema de las neuronas inactivas.

4.6 Determinación de las funciones de activación candidatas

La selección de la función de activación es una de las decisiones más importantes en el diseño de redes neuronales. Las funciones de activación tienen un impacto directo en la capacidad de la red para aprender patrones complejos, la velocidad de entrenamiento y el rendimiento general. A continuación se presentan los resultados de investigaciones recientes y mejores prácticas según el campo de aplicación.

Visión por computadora (Computer Vision)

Modelos basados en CNN: ReLU y sus variantes (LeakyReLU, PReLU, ELU) siguen siendo ampliamente utilizadas debido a su alta eficiencia computacional y buen rendimiento general. Sin embargo, GELU y Swish/SiLU se están utilizando cada vez más en arquitecturas más profundas, especialmente en CNN de alto rendimiento, debido a sus gradientes más suaves.
Transformadores de visión (ViTs): En ViT, GELU se ha establecido prácticamente como estándar. Esto es coherente con el uso exitoso de GELU en transformadores del campo de procesamiento de lenguaje natural.
Dispositivos móviles/empotrados: Hardswish es preferido en entornos con recursos limitados debido a su eficiencia computacional. ReLU y sus variantes (como ReLU6, comúnmente utilizada en MobileNets) también siguen siendo opciones sólidas.
Modelos generativos (generación de imágenes de alta precisión): Aunque STAF ha mostrado resultados prometedores, aún no se ha adoptado ampliamente. Funciones de activación suaves como Swish, GELU y Mish son más preferidas en tareas de generación debido a su tendencia a producir resultados de mayor calidad y reducir los artefactos. Los modelos de difusión (Diffusion), que representan el estado del arte actual en la generación de imágenes, a menudo utilizan Swish/SiLU.

Procesamiento del lenguaje natural (NLP)

Modelos basados en transformadores: GELU es la elección dominante en la mayoría de las arquitecturas de transformadores (BERT, GPT, etc.).
RNN/LSTM: Históricamente, Tanh ha sido preferido, pero gradualmente está siendo reemplazado por funciones de activación que mitigan mejor el problema del desvanecimiento del gradiente. GELU y variantes de ReLU (junto con técnicas cuidadosas de inicialización y regularización) se utilizan frecuentemente en implementaciones modernas de RNN/LSTM.
Modelos de lenguaje a gran escala (LLMs): La eficiencia computacional es crucial. GELU y ReLU (o aproximaciones rápidas de GELU) son las opciones más comunes. Algunos LLMs experimentan con funciones de activación especiales dentro de capas de mezcla de expertos (Mixture-of-Experts, MoE).

Procesamiento de voz (Speech Processing)

Reconocimiento emocional: Aunque Teacup ha mostrado resultados prometedores, aún no se ha adoptado ampliamente. Funciones de activación suaves como Swish y GELU son candidatas sólidas para CNN debido a sus gradientes más suaves.
Síntesis de voz: Funciones de activación suaves como Snake y GELU a menudo se recomiendan ya que pueden ayudar a generar voces más naturales.
Procesamiento en tiempo real: Similar a la visión móvil, Hardswish y variantes de ReLU son adecuadas para aplicaciones que requieren tiempos de latencia bajos.

Recomendaciones generales y tendencias actuales

A continuación se presenta un enfoque más sistemático para seleccionar funciones de activación candidatas.

Selección básica (buen punto de partida):
- GELU: Excelente opción versátil, especialmente para transformadores y redes más profundas.
- ReLU (o LeakyReLU/PReLU): Todavía es una opción sólida y eficiente para CNN. Considere usar LeakyReLU o PReLU para evitar el problema de “ReLU muerto”.
- Swish/SiLU: A menudo supera a ReLU en redes más profundas y ofrece un buen rendimiento general en varios aspectos.
Alto rendimiento (potencialmente más cálculos):
- Mish: A menudo logra los mejores resultados, pero tiene un costo de cálculo mayor que ReLU o GELU.
- TeLU: Es una variación aprendible de ELU. Las afirmaciones sobre una convergencia más rápida y estabilidad valen la pena ser verificadas, aunque aún no ha sido ampliamente adoptada. El benchmarking es fundamental.
- Funciones de Activación Racionales: Tienen la capacidad de aproximar funciones complejas y manejar sistemas dinámicos, lo que las hace prometedoras para el aprendizaje por refuerzo y redes neuronales basadas en física (PINN). Sin embargo, se utilizan menos comúnmente en tareas de aprendizaje supervisado estándar.
Ligero/eficiente:
- Hardswish: Diseñado para dispositivos móviles y embebidos.
- ReLU6: Una variación de ReLU que limita el rango de salida a 6, se utiliza comúnmente en modelos cuantificados.
Adaptativo/aprendible:
- PReLU: Aprende la pendiente negativa. Es simple y efectiva.
- TeLU: Aprende un factor de escala para la parte exponencial de la función ELU.
- STAF: Muestra potencial para capturar patrones complejos, pero STAF (y otras activaciones basadas en Fourier) son costosas computacionalmente y aún no han demostrado una superioridad consistente sobre opciones más simples en la mayoría de las tareas comunes. Siguen siendo un área de investigación activa.
- B-spline: La propiedad de control local es interesante, pero las activaciones B-spline (similar a STAF) son menos comunes en el aprendizaje profundo mainstream debido a su complejidad. Se ven más frecuentemente en aplicaciones especializadas como ajuste de curvas o modelado geométrico. Es un área de investigación activa y puede ser eficaz para el aprendizaje continuo/ incremental, aunque aún no hay resultados ampliamente establecidos.

Principales tendencias y consideraciones recientes:

Reducción del uso de Sigmoid/Tanh en redes profundas: Debido al problema de la desaparición del gradiente, rara vez se utilizan como activaciones de capa oculta en redes neuronales modernas.
Importancia de la suavidad (Smoothness): Las funciones de activación suaves (GELU, Swish, Mish) son generalmente preferidas sobre las no suaves (ReLU) en redes más profundas. Esto se debe a que tienden a conducir a un entrenamiento más estable y un mejor flujo del gradiente.
Costo computacional: En particular para modelos grandes o dispositivos con recursos limitados, siempre considere el costo de cálculo de las funciones de activación.
Especificidad de la tarea (Task Specificity): La función de activación óptima puede variar significativamente según la tarea. Es importante realizar experimentos.
Mezcla de expertos (Mixture of Experts, MoE): En modelos muy grandes como algunos LLM, diferentes funciones de activación pueden ser utilizadas dentro de diferentes subredes “expertas”.
Funciones de activación racionales y sistemas dinámicos: La capacidad de las funciones de activación racionales y sus extensiones “joint-rational” para aprender y representar la dinámica del sistema es una línea de investigación prometedora.

Lo más importante es siempre experimentar! Comience con un valor razonable por defecto (GELU o ReLU/LeakyReLU), pero esté preparado para probar otras opciones si no logra el rendimiento deseado. Pequeños experimentos donde solo cambia la función de activación, manteniendo otros hiperparámetros constantes, son esenciales para tomar decisiones informadas.

Haz clic para ver el contenido (deep dive: diseñar tu propia función de activación)

Buceo profundo: Diseñando tu propia función de activación - Teoría y práctica

La función de activación es uno de los componentes clave de un modelo de aprendizaje profundo y tiene un gran impacto en la capacidad expresiva del modelo, la velocidad de aprendizaje y el rendimiento final. Además de las funciones de activación comúnmente utilizadas (ReLU, GELU, Swish, etc.), numerosos investigadores han propuesto nuevas funciones de activación. En este buceo profundo, examinaremos paso a paso el proceso de diseñar tu propia función de activación y aprenderemos cómo implementarla y probarla usando PyTorch.

1. Principios básicos del diseño de funciones de activación

Antes de diseñar una nueva función de activación, repasemos las condiciones de la “función de activación ideal” descritas en el apartado 4.2.

No linealidad (Non-linearity): Permite que las redes neuronales representen funciones complejas.
Diferenciabilidad (Differentiability): Es esencial para entrenar redes neuronales mediante el algoritmo de retropropagación (backpropagation). Se permiten funciones no diferenciables en algunos puntos, como ReLU.
Prevención del problema de desvanecimiento y explosión de gradientes: Asegura que el aprendizaje sea estable en redes neuronales profundas.
Eficiencia computacional (Computational Efficiency): Afecta la velocidad de entrenamiento e inferencia de las redes neuronales.

Además, se pueden considerar los siguientes aspectos:

Salida centrada en cero (Zero-Centered Output): Una salida de función de activación centrada en cero puede mejorar la velocidad de aprendizaje. (Tanh, ELU)
Auto-gating: Característica por la cual el grado de activación se ajusta según el valor de entrada. (Swish)
Suavidad (Smoothness): Las funciones de activación suaves generalmente llevan a un aprendizaje más estable.
Monotonicidad (Monotonicity): Una función monotónica es aquella cuya salida aumenta o disminuye a medida que la entrada lo hace. ReLU, Leaky ReLU, ELU, GELU, Swish, Mish son todas funciones monótonas. Sigmoid y Tanh no son funciones monótonas. La monotonicidad puede facilitar la optimización, pero no es un requisito indispensable.
Limitación (Boundedness): Indica si la salida de la función de activación está restringida a un rango específico. Sigmoid y Tanh son funciones limitadas, mientras que las variantes ReLU son ilimitadas. Las funciones limitadas pueden ayudar a prevenir la explosión del gradiente, pero también pueden limitar la capacidad expresiva.

2. Generación de ideas: Combinación y modificación de funciones de activación existentes

El método más común para diseñar una nueva función de activación es combinar o modificar funciones de activación existentes.

Variaciones basadas en ReLU: Para abordar el problema del “Dying ReLU,” se han propuesto varias variaciones como Leaky ReLU, PReLU, ELU y SELU. Estas ideas pueden extenderse para cambiar el comportamiento en la región negativa o agregar parámetros aprendibles.
Variaciones basadas en Sigmoid/Tanh: Para mitigar el problema del desvanecimiento de gradientes, se pueden considerar modificaciones a las funciones Sigmoid y Tanh, o combinarlas con otras funciones.
Series Swish/Mish: Swish(\(x \cdot sigmoid(x)\)) y Mish(\(x \cdot tanh(ln(1 + e^x))\)) son conocidas por mostrar buen rendimiento. Se pueden considerar modificaciones a estas funciones o su combinación con otras.
Variaciones basadas en GELU: GELU es ampliamente utilizada en modelos Transformer. Se pueden modificar las aproximaciones de GELU o combinarlas con otras funciones para crear nuevas funciones de activación.

3. Análisis matemático: Diferenciabilidad, características de gradientes

Si se propone una nueva función de activación, es necesario realizar un análisis matemático.

Diferenciabilidad: Se debe verificar si la función propuesta es diferenciable en todos los intervalos, o si, como ReLU, no es diferenciable en algunos puntos pero puede definir subgradientes. Usar la funcionalidad de diferenciación automática de PyTorch para calcular valores derivados y graficarlos puede ser útil.
Características del gradiente: Se debe analizar cómo cambia el gradiente según el rango de los valores de entrada. Se deben verificar si existen regiones donde el gradiente se vuelve demasiado pequeño (gradiente desaparecido) o demasiado grande (gradiente explotando).

4. Implementación en PyTorch

Una función de activación que ha sido validada por análisis matemático puede implementarse fácilmente usando PyTorch. Se debe crear una nueva clase heredando de torch.nn.Module y definir la operación de la función de activación en el método forward. Si es necesario, se pueden definir parámetros entrenables con torch.nn.Parameter.

Ejemplo: Implementación de la función de activación “SwiGELU”

Vamos a proponer e implementar una nueva función de activación llamada “SwiGELU”, que combina Swish y GELU. (Basado en ideas del problema 4.2.3)

import torch
import torch.nn as nn
import torch.nn.functional as F

class SwiGELU(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, x):
        return 0.5 * (x * torch.sigmoid(x) + F.gelu(x))

Explicación:

SwiGELU(x) = 0.5 * (x * sigmoid(x) + GELU(x))
Se combinan Swish(\(x \cdot sigmoid(x)\)) y GELU(\(x\Phi(x)\)) en una proporción de 1:1, y se multiplica por 0.5 para ajustar el rango de salida.
Se espera poder aprovechar tanto la característica de puerta propia de Swish como la no linealidad suave y los efectos de regularización de GELU.

5. Experimentación y evaluación

Si se propone una nueva función de activación, es necesario realizar experimentos para comparar su rendimiento con funciones de activación existentes utilizando conjuntos de datos de referencia (por ejemplo, CIFAR-10, CIFAR-100, ImageNet).

Configuración del experimento:
- Se utiliza la misma arquitectura de modelo y se cambia solo la función de activación.
- Otros hiperparámetros como tasa de aprendizaje, tamaño del lote, optimizador, etc., se mantienen constantes.
- Se repiten varios experimentos para asegurar la significancia estadística de los resultados.
Métricas de evaluación:
- Precisión
- Pérdida
- Tiempo de entrenamiento
- Velocidad de convergencia
- Norma del gradiente - Utilizar la función train_model_with_metrics
- Número/porcentaje de neuronas deshabilitadas (“neuronas muertas”) - Utilizar la función calculate_disabled_neuron
- Otras métricas, como el uso de memoria, si es necesario.
Análisis de resultados
- Comparación cuantitativa de la velocidad de convergencia y el rendimiento final
- Verificación de problemas de gradiente desaparecido/explotando
- Tasa de ocurrencia de “neuronas muertas”

6. (Opcional) Análisis teórico

Si los resultados experimentales son buenos, es recomendable realizar un análisis teórico para comprender por qué la nueva función de activación muestra un mejor rendimiento. * Análisis del paisaje de pérdidas: analiza el impacto que tiene la función de activación en el espacio de la función de pérdida (loss landscape). (Ver sección 4.2 Deep Dive) * Análisis del Kernel Tangente Neural (NTK): examina el papel de la función de activación en redes neuronales infinitamente anchas. * Ecuación de Fokker-Planck: analiza las características dinámicas de la función de activación. (Ver estudios sobre Swish)

Conclusión

Diseñar y evaluar nuevas funciones de activación es una tarea desafiante, pero es un campo de investigación con gran potencial para mejorar el rendimiento de los modelos de deep learning. Superar las limitaciones de las funciones de activación existentes y encontrar funciones de activación más adecuadas para problemas o arquitecturas específicas es uno de los desafíos más importantes en la investigación de deep learning. Se espera que el enfoque paso a paso presentado en este Deep Dive, junto con ejemplos de implementación en PyTorch y directrices para experimentación y análisis, ayuden a diseñar sus propias funciones de activación.

Haga clic para ver el contenido (deep dive: funciones de activación adaptativas - direcciones futuras de investigación)

Buceo profundo: funciones de activación adaptativas - direcciones futuras de investigación

Introducción:

Las funciones de activación fijas como ReLU y GELU son ampliamente utilizadas en modelos de deep learning, pero pueden no estar optimizadas para problemas específicos o distribuciones de datos. Recientemente, se ha llevado a cabo una investigación intensa sobre el ajuste adaptativo de funciones de activación según los datos o la tarea. En este buceo profundo, exploramos el potencial y las direcciones futuras de investigación de las funciones de activación adaptativas (Adaptive Activation Function).

1. Tipos de funciones de activación adaptativas

Las funciones de activación adaptativas se pueden clasificar en general de la siguiente manera.

Ajuste paramétrico (Parametric Adaptation): Se introducen parámetros aprendibles en la función de activación para ajustar su forma según los datos.
- Ejemplos:
  - Leaky ReLU: \(f(x) = max(\\alpha x, x)\) (\(\\alpha\) es un parámetro aprendible)
  - PReLU (Parametric ReLU): Se aprende \(\\alpha\) para cada canal en lugar de una constante
  - Swish: \(f(x) = x \\cdot \\sigma(\\beta x)\) (\(\\beta\) es un parámetro aprendible)
Ajuste estructural (Structural Adaptation): Se combinan varias funciones base o se modifica la arquitectura de la red para construir dinámicamente la función de activación.
- Ejemplos:
  - Redes Maxout: Se selecciona el valor máximo entre múltiples funciones lineales
  - Funciones de activación basadas en splines: Se utilizan funciones spline para representar la función de activación
Ajuste basado en entrada: Se cambia o combina la función de activación según las características de los datos de entrada.
- Ejemplos:
  - Bloque Squeeze and Excitation (SE): Se calcula la importancia entre los canales de las características de entrada y se aplica un peso a la función de activación

2. Posibles direcciones de investigación

2.1 Funciones de activación basadas en Mixture of Experts (MoE)

Idea: Se definen múltiples funciones de activación “expertas” y se determinan dinámicamente los pesos de cada experto según los datos de entrada.
Expresión matemática:

\(f(x) = \\sum\_{k=1}^K g\_k(x) \\cdot \\phi\_k(x)\)
- \(g\_k(x)\): Función de puerta (gating function) para la k-ésima función de activación experta, normalizada mediante softmax u otros métodos
- \(\\phi\_k(x)\): La k-ésima función de activación experta (pueden usarse funciones como ReLU, GELU, Swish, entre otras)
Tareas de investigación:
- Mecanismos eficientes de puerta: Estudio de métodos eficientes para calcular \(g\_k(x)\) (ejemplo: Top-k gating, sparse gating)
- Selección de funciones de activación expertas: Investigación sobre qué tipo de \(\\phi\_k(x)\) es mejor usar y cómo determinar el número de expertos
- Análisis teórico: Análisis teórico del poder expresivo (expressive power) y la capacidad de generalización de las funciones de activación MoE

2.2 Integración con búsqueda de arquitectura neural (Neural Architecture Search, NAS)

Idea: Utilizar NAS para explorar automáticamente la estructura de funciones de activación optimizadas para los datos y tareas.
Enfoque:
- Espacio de búsqueda (Search Space):
  - Definir operaciones básicas (transformaciones lineales, funciones exponenciales, logarítmicas, trigonométricas, etc.)
  - Definir una variedad de candidatos a funciones de activación que se pueden crear combinando estas operaciones.
- Estrategia de búsqueda (Search Strategy):
  - Aprendizaje por refuerzo (Reinforcement Learning)
  - Algoritmos evolutivos (Evolutionary Algorithm)
  - Búsqueda de arquitectura diferenciable (Differentiable Architecture Search, DARTS)
- Evaluación del rendimiento (Performance Estimation):
  - Entrenar y evaluar el rendimiento en un conjunto de datos de validación de modelos que incluyen las funciones de activación encontradas.
Tareas de investigación:
- Diseño eficiente del espacio de búsqueda: Definir un espacio de búsqueda lo suficientemente diverso pero no excesivamente grande para incluir una variedad de funciones de activación.
- Reducción del costo computacional: Dado que NAS es muy costoso en términos de cálculo, desarrollar estrategias eficientes de búsqueda y métodos de evaluación del rendimiento.

2.3 Integración de información física/biológica

Idea: Utilizar el conocimiento del dominio en campos como la física y la biología para imponer restricciones o knowledge prior en el diseño de funciones de activación.
Ejemplos:
- Modelo físico: Al modelar un sistema físico específico, reflejar las ecuaciones diferenciales del sistema en la función de activación.
- Neurociencia: Funciones de activación que imitan el funcionamiento de los verdaderos neuronas (por ejemplo, modelos de neuronas con disparo).
Tareas de investigación:
- Integración efectiva del conocimiento del dominio: Desarrollar metodologías para reflejar el conocimiento del dominio en el diseño de funciones de activación.
- Rendimiento general: Verificar si las funciones de activación especializadas en un dominio específico funcionan bien en otros dominios.

2.4 Reforzamiento del análisis teórico

Potencia expresiva (Expressive Power): Analizar cuán más potentes son las funciones de activación adaptativas en comparación con las funciones de activación tradicionales.
Facilidad de optimización (Optimization Landscape): Analizar cómo las funciones de activación adaptativas modifican la superficie de la función de pérdida y qué impacto tiene esto en la velocidad y estabilidad del aprendizaje.
Rendimiento general (Generalization): Analizar si las funciones de activación adaptativas previenen el sobreajuste y mejoran el rendimiento general.

3. Conclusión y recomendaciones

Las funciones de activación adaptativas son un campo de investigación prometedor para mejorar el rendimiento de los modelos de aprendizaje profundo. Sin embargo, quedan desafíos pendientes:

Complejidad computacional: Las funciones de activación adaptativas suelen ser más costosas en términos de cálculo que las funciones de activación fijas.
Interpretabilidad: A medida que la forma de las funciones de activación aprendidas se vuelve más compleja, puede volverse difícil interpretar el modelo.
Riesgo de sobreajuste: Las funciones de activación demasiado flexibles pueden sobreajustarse a los datos de entrenamiento.

Es importante que futuras investigaciones aborden estos desafíos para desarrollar funciones de activación adaptativas más eficientes, interpretables y con un rendimiento general superior.

Ejercicios de práctica

4.2.1 Problemas básicos

Escriba las fórmulas y grafique las funciones Sigmoid, Tanh, ReLU, Leaky ReLU, GELU, Swish. (utilice matplotlib, Desmos, etc.)
- Referencia: Asegúrese de entender claramente la definición y características de cada función, y compare visualmente a través de los gráficos.
Calcule las derivadas (funciones derivadas) de cada función de activación y grafíquelas.
- Referencia: Las derivadas se utilizan para calcular gradientes en el proceso de retropropagación. Determine la diferenciabilidad de cada función y las características del gradiente.
Utilice el conjunto de datos FashionMNIST para entrenar una red neuronal compuesta solo por transformaciones lineales sin funciones de activación, y mida la precisión de prueba. (utilice SimpleNetwork implementado en el Capítulo 1)
- Referencia: Una red neuronal sin funciones de activación no puede representar nonlinearidades, lo que limita su capacidad para resolver problemas complejos. Verifique esto a través del experimento.
Compare los resultados obtenidos en el problema 3 con los resultados de una red neuronal que utiliza la función de activación ReLU, y explique el papel de las funciones de activación.
- Referencia: Compare y explique los valores de salida por capa, los gradientes y las neuronas inactivas cuando hay y no hay función de activación.

4.2.2 Problemas aplicados

Implemente las funciones de activación PReLU, TeLU, STAF en PyTorch. (herede nn.Module)
- Referencia: Consulte la definición de cada función y implemente el método forward. Defina parámetros aprendibles con nn.Parameter si es necesario.
Utilice el conjunto de datos FashionMNIST para entrenar una red neuronal que incluya las funciones de activación implementadas anteriormente, y compare la precisión de prueba.
- Referencia: Compare el rendimiento de cada función de activación y analice cuál es más adecuada para el conjunto de datos FashionMNIST.
Visualice la distribución de gradientes durante el entrenamiento para cada función de activación, y mida la proporción de “neuronas muertas”. (utilice las funciones implementadas en el Capítulo 1)
- Referencia: Compare la distribución de gradientes entre los valores iniciales y los entrenados, y por capa, para cada función de activación.
Investigue y explique los métodos para mitigar el problema de “neuronas muertas”. (Leaky ReLU, PReLU, ELU, SELU, etc.)
- Referencia: Explique cómo cada método aborda las limitaciones de ReLU, y cuáles son sus ventajas y desventajas.

4.2.3 Problemas avanzados

Implemente la función de activación Rational en PyTorch y explique sus características y ventajas y desventajas.
- Referencia: La función de activación Rational se basa en funciones racionales (funciones fraccionarias) y puede mostrar un rendimiento superior a otras funciones de activación en problemas específicos.
Implemente la función de activación B-spline o Fourier-based en PyTorch y explique sus características y ventajas y desventajas.
- Referencia: La función de activación B-spline puede representar curvas flexibles controladas localmente, mientras que la función de activación basada en Fourier es útil para modelar patrones periódicos.
Proponga una nueva función de activación propia y evalúe su rendimiento comparándola con las funciones de activación existentes. (presente resultados experimentales y justificación teórica)
- Referencia: Al diseñar una nueva función de activación, considere los criterios ideales para una función de activación (nonlinearidad, diferenciabilidad, prevención de problemas de desvanecimiento/explotación del gradiente, eficiencia computacional, etc.).

Haga clic para ver el contenido (solución)

Soluciones de Ejercicios

4.2.1 Problemas Básicos

1. Fórmulas y gráficas de las funciones Sigmoid, Tanh, ReLU, Leaky ReLU, GELU, Swish:

| Función de Activación | Fórmula        | Gráfico (Referencia)    |
| ------- | ------------------------------------------------------- | ---------------------------------------------------- |
| Sigmoid     | $\sigma(x) = \frac{1}{1 + e^{-x}}$                                         | [Sigmoid](https://www.google.com/search?q=https://upload.wikimedia.org/wikipedia/commons/thumb/8/88/Logistic-curve.svg/320px-Logistic-curve.svg.png) |
| Tanh        | $tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}$                           | [Tanh](https://www.google.com/search?q=https://upload.wikimedia.org/wikipedia/commons/thumb/c/c7/Hyperbolic_Tangent.svg/320px-Hyperbolic_Tangent.svg.png)     |
| ReLU        | $ReLU(x) = max(0, x)$                                                     | [ReLU](https://www.google.com/search?q=https://upload.wikimedia.org/wikipedia/commons/thumb/f/fe/Activation_rectified_linear.svg/320px-Activation_rectified_linear.svg.png) |
| Leaky ReLU  | $LeakyReLU(x) = max(ax, x)$ ,  ($a$ es una constante pequeña, generalmente 0.01)               | (Leaky ReLU tiene una pequeña pendiente($a$) en la parte donde x < 0 del gráfico de ReLU)                  |
| GELU        | $GELU(x) = x\Phi(x)$ , ($\Phi(x)$ es la función de distribución acumulativa gaussiana)             | [GELU](https://www.google.com/search?q=https://production-media.paperswithcode.com/methods/Screen_Shot_2020-06-22_at_3.34.27_PM_fufBJEx.png)            |
| Swish       | $Swish(x) = x \cdot sigmoid(\beta x)$ , ($\beta$ es una constante o un parámetro de aprendizaje) | [Swish](https://www.google.com/search?q=https://production-media.paperswithcode.com/methods/Screen_Shot_2020-06-22_at_3.35.27_PM_d7LqDQj.png)          |

2. Derivadas (funciones derivadas) de cada función de activación:

función de activación	derivada
Sigmoid	\(\sigma'(x) = \sigma(x)(1 - \sigma(x))\)
Tanh	\(tanh'(x) = 1 - tanh^2(x)\)
ReLU	\(ReLU'(x) = \begin{cases} 0, & x < 0 \\ 1, & x > 0 \end{cases}\)
Leaky ReLU	\(LeakyReLU'(x) = \begin{cases} a, & x < 0 \\ 1, & x > 0 \end{cases}\)
GELU	\(GELU'(x) = \Phi(x) + x\phi(x)\), (\(\phi(x)\) es la función de densidad de probabilidad gaussiana)
Swish	\(Swish'(x) = sigmoid(\beta x) + x \cdot sigmoid(\beta x)(1 - sigmoid(\beta x))\beta\)

Entrenamiento y medición de precisión de una red neuronal sin función de activación en FashionMNIST:
- Una red neuronal sin función de activación solo realiza transformaciones lineales, por lo que no puede modelar relaciones no lineales complejas. Por lo tanto, muestra una baja precisión en conjuntos de datos complejos como FashionMNIST (aproximadamente 10% de precisión).
Comparación con una red neuronal que utiliza la función de activación ReLU, y explicación del papel de las funciones de activación:
- Una red neuronal que utiliza la función de activación ReLU introduce no linealidad, lo que permite alcanzar una precisión mucho mayor (más del 80%).
- Salidas por capa: Sin función de activación, la distribución de las salidas por capa muestra solo un cambio de escala simple. Con ReLU, los valores negativos se suprimen a 0, lo que cambia la distribución.
- Gradientes: Sin función de activación, los gradientes se transmiten simplemente. Con ReLU, para entradas negativas, el gradiente es 0 y no se propaga.
- Neuronas inactivas: No ocurren cuando no hay función de activación, pero pueden ocurrir al usar ReLU.
- Resumen del papel: Las funciones de activación otorgan no linealidad a la red neuronal, permitiendo aproximar funciones complejas y regulando el flujo de gradientes para facilitar el aprendizaje.

4.2.2 Problemas de aplicación

Implementación de PReLU, TeLU, STAF en PyTorch:

import torch
import torch.nn as nn

class PReLU(nn.Module):
    def __init__(self, num_parameters=1, init=0.25):
        super().__init__()
        self.alpha = nn.Parameter(torch.full((num_parameters,), init))

    def forward(self, x):
        return torch.max(torch.zeros_like(x), x) + self.alpha * torch.min(torch.zeros_like(x), x)

```python import torch import torch.nn as nn

class TeLU(nn.Module): def init(self, alpha=1.0): super().__init__() self.alpha = nn.Parameter(torch.tensor(alpha))

def forward(self, x):
    return torch.where(x > 0, x, self.alpha * (torch.exp(x) - 1))

class STAF(nn.Module): def init(self, tau=25): super().__init__() self.tau = tau self.C = nn.Parameter(torch.randn(tau)) self.Omega = nn.Parameter(torch.randn(tau)) self.Phi = nn.Parameter(torch.randn(tau))

def forward(self, x):
    result = torch.zeros_like(x)
    for i in range(self.tau):
        result += self.C[i] * torch.sin(self.Omega[i] * x + self.Phi[i])
    return result


2.  **Comparación de funciones de activación en FashionMNIST:**

    *   Se entrenan redes neuronales que incluyen PReLU, TeLU y STAF, y se comparan las precisiones de prueba.
    *   Los resultados del experimento muestran una tendencia a que las funciones de activación adaptativas (PReLU, TeLU, STAF) tengan mayor precisión que ReLU. (STAF > TeLU > PReLU > ReLU)

3.  **Visualización de la distribución del gradiente y medición de la proporción de "neuronas muertas":**

    *   ReLU tiene un gradiente de 0 para entradas negativas, mientras que PReLU, TeLU y STAF propagan pequeños valores de gradiente incluso para entradas negativas.
    *   La proporción de "neuronas muertas" es más alta en ReLU y más baja en PReLU, TeLU y STAF.

4.  **Métodos y principios para aliviar el problema de las "neuronas muertas":**

    *   **Leaky ReLU:** Permite una pequeña pendiente para entradas negativas, evitando que las neuronas se desactiven por completo.
    *   **PReLU:** Convierte la pendiente de Leaky ReLU en un parámetro aprendible, ajustándola óptimamente según los datos.
    *   **ELU, SELU:** Tienen valores no nulos en el dominio negativo y una forma curva suave, lo que ayuda a mitigar el problema del desvanecimiento del gradiente y estabiliza el aprendizaje.

### 4.2.3 Problemas avanzados

1.  **Implementación de la función de activación Rational en PyTorch, características y ventajas y desventajas:**

    ```python
    import torch
    import torch.nn as nn

    class Rational(nn.Module):
        def __init__(self, numerator_coeffs, denominator_coeffs):
            super().__init__()
            self.numerator_coeffs = nn.Parameter(numerator_coeffs)
            self.denominator_coeffs = nn.Parameter(denominator_coeffs)

def forward(self, x):
    numerator = torch.polyval(self.numerator_coeffs, x) # cálculo polinomial
    denominator = 1 + torch.polyval(self.denominator_coeffs, torch.abs(x))  # valor absoluto y cálculo polinomial
    return numerator / denominator

Característica: Forma de función racional (función fraccional). El numerador y el denominador se representan con polinomios.
Ventaja: Forma flexible de la función. Puede ofrecer un rendimiento superior a otras funciones de activación en problemas específicos.
Desventaja: Debe tener cuidado para evitar que el denominador sea cero. Es necesario ajustar los hiperparámetros (coeficientes del polinomio).

Implementación, características y ventajas/desventajas de funciones de activación basadas en B-splines o Fourier:

Función de activación B-spline:

import torch
import torch.nn as nn
from scipy.interpolate import BSpline
import numpy as np

class BSplineActivation(nn.Module):
    def __init__(self, knots, degree=3):
        super().__init__()
        self.knots = knots
        self.degree = degree
        self.coeffs = nn.Parameter(torch.randn(len(knots) + degree - 1)) # puntos de control

    def forward(self, x):
        # Cálculo del B-spline
        b = BSpline(self.knots, self.coeffs.detach().numpy(), self.degree) # usar coeficientes separados
        spline_values = torch.tensor(b(x.detach().numpy()), dtype=torch.float32) # ingresar x en el B-spline
        return spline_values * self.coeffs.mean() # si no se usa detach, numpy() se produce un error
         # si no se usa detach, numpy() se produce un error

Característica: Curva flexible controlada localmente. La forma se ajusta mediante nudos (knots) y grado (degree).
Ventaja: Expresión de función suave. Aprendizaje de características locales.
Desventaja: El rendimiento puede verse afectado por la configuración de los nudos. Aumento de la complejidad computacional.

Propuesta y evaluación del rendimiento de una nueva función de activación:
- (Ejemplo) Función de activación que combina Swish y GELU:
```
import torch
import torch.nn as nn
import torch.nn.functional as F
class SwiGELU(nn.Module): # Swish + GELU
  def forward(self, x):
    return 0.5 * (x * torch.sigmoid(x) + F.gelu(x))
```
  SwiGELU combina la suavidad de Swish con el efecto de normalización de GELU.
- Diseño experimental y evaluación del rendimiento: Comparar con funciones de activación existentes en conjuntos de datos de referencia como FashionMNIST. (Se omiten los resultados experimentales) ```

Referencias

Deep Learning (Goodfellow, Bengio, Courville, 2016): Capítulo 6.3 (Funciones de Activación) https://www.deeplearningbook.org/
- Un libro de texto que abarca una amplia gama de temas en deep learning. Además de los conceptos básicos de las funciones de activación, también se pueden aprender otros conceptos importantes del deep learning.
Understanding the difficulty of training deep feedforward neural networks (Glorot & Bengio, 2010) http://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf
- Un artículo que analiza el problema de la desaparición del gradiente en las funciones de activación Sigmoid y Tanh, y propone el método de inicialización Xavier. Es un recurso importante para entender las dificultades en el entrenamiento de redes neuronales profundas.
Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification (He et al., 2015) https://arxiv.org/abs/1502.01852
- Un artículo que propone las funciones de activación ReLU y PReLU, así como el método de inicialización He. Ayuda a comprender mejor las funciones de activación ReLU, ampliamente utilizadas en deep learning moderno.
Searching for Activation Functions (Ramachandran et al., 2017) https://arxiv.org/abs/1710.05941
- Un artículo que descubre la función de activación Swish a través de la búsqueda de arquitecturas neuronales (Neural Architecture Search, NAS). Proporciona ideas sobre cómo explorar nuevas funciones de activación.
STAF: A Sinusoidal Trainable Activation Function for Deep Learning (Jeon & Cho, 2025) https://arxiv.org/abs/2405.13607
- Un artículo presentado en ICLR 2025 que propone STAF, una función de activación aprendible basada en la serie de Fourier. Ayuda a comprender las últimas tendencias en investigación sobre funciones de activación adaptativas.